Um bloco de parte do repouso sobre um plano inclinado rugoso que faz um ângulo de com a horizontal. O coeficiente de atrito cinético entre o bloco e o plano é . Quando o bloco desce ao longo do plano, a energia mecânica do sistema Terra-bloco:
Dado: (capa da prova)
(A) aumenta de ;
(B) diminui de ;
(C) não se altera
(D) diminui de ;
(E) aumenta de ;
Passo 1
Um bloco desce um plano inclinado...
Até ai, padrão.
Imagina se não houvesse atrito...
A energia potencial ia sendo convertida em energia cinética , a medida que o corpo desce a rampa. Mas no saldo final a energia mecânica (total) se conserva.
Porém, temos atrito...
A energia na forma de se convertendo em ainda vai ocorrer. Porém, como temos uma força dissipativa (atrito), uma parte dessa energia será perdida.
Mas quanto, exatamente?
A quantidade de energia perdida é dada pelo trabalho dessa força dissipativa , e como essa quantidade de energia foi retirada da energia total , temos que o trabalho dessa força é o quanto a energia mecânica variou:
Então, basta a gente calcular o trabalho da força de atrito que conseguimos nossa resposta.
Passo 2
Sobre o arranjo de forças, temos a seguinte situação:
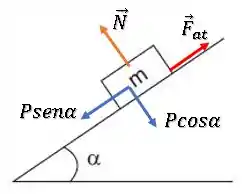
O bloco se desloca para baixo do plano e a força de atrito está contrária ao movimento, então seu trabalho é dado por:
Já temos o valor do coeficiente de atrito cinético e do deslocamento . Só falta o valor da Normal .
Como o bloco está em equilíbrio na direção perpendicular ao plano, podemos dizer que as forças nessa direção se anulam, logo:
O peso do bloco é dado por , enquanto a inclinação da pista :
Então, temos que:
Calculando esse cosseno, temos:
Então, achamos que a variação da energia mecânica é:
Ou seja, a energia mecânica diminuiu de .
Resposta
Letra (B)