Um bloco desce um plano inclinado com velocidade constante. Atuam sobre o bloco, além da força peso, apenas as forças normal e de atrito devidas ao contato entre o bloco e a superfície do plano. Em um deslocamento que o bloco realiza sobre o plano, pode-se afirmar que:
(a) O trabalho realizado pela força de atrito é positivo.
(b) O trabalho realizado pela força peso é negativo.
(c) O trabalho realizado pela força resultante sobre o bloco é positivo.
(d) O trabalho realizado pela força resultante sobre o bloco é nulo.
(e) O trabalho realizado pela força normal é negativo.
Passo 1
Dá uma olhada aqui no desenho da situação.
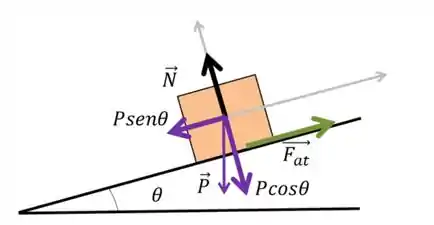
A informação mais importante do nosso enunciado é que o bloco está descendo a rampa com uma velocidade constante, pois isso significa que o somatório de forças sobre ele é nulo, já que ele não tem aceleração ().
Além disso, lembra que trabalho é a força vezes o deslocamento e isso vezes o cosseno do ângulo () entre eles?
Agora, vamos analisar cada alternativa.
Passo 2
(a) O trabalho realizado pela força de atrito é positivo.
(b) O trabalho realizado pela força peso é negativo.
Dá uma olhada na figura um pouco mais simplificada aqui.
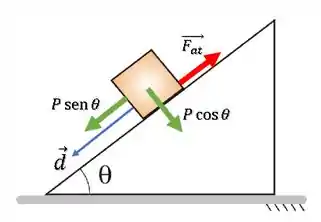
A força peso () está decomposta nas componentes paralela e perpendicular à superfície da rampa.
A componente é perpendicular ao deslocamento (), logo o ângulo entre eles é , então o trabalho da componente é nulo.
Já a componente está na mesma direção e no mesmo dentido do deslocamento (), então o ângulo () entre eles é zero.
Assim, o trabalho da força peso é positivo.
Agora, vamos à força de atrito. Ela está contra o movimento (mesma direção e sentidos opostos). Assim, o ângulo entre a força e o deslocamento () é . Logo, seu trabalho será:
Então, o trabalho da é negativo.
As letras (a) e (b) estão erradas.
Passo 3
(c) O trabalho realizado pela força resultante sobre o bloco é positivo.
(d) O trabalho realizado pela força resultante sobre o bloco é nulo.
A gente viu que se a velocidade do bloco é constante, a força resultante é zero, então:
Letra (d) está correta e a letra (c) está errada.
Vamos ver a última pra confirmar! Por que não, né?
Passo 4
(e) O trabalho realizado pela força normal é negativo.
Sobre a força normal:
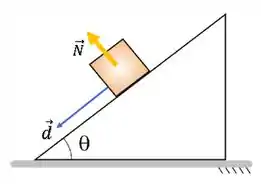
Ela é perpendicular ao deslocamento do bloco, então seu trabalho também será nulo.
A letra (e) está errada.
Resposta
Letra (d)