Uma partícula é deslocada de no sentido negativo do eixo x mediante a aplicação da força constante . Qual o trabalho realizado por essa força sobre a partícula?
(A)
(B)
(C)
(D)
(E)
Passo 1
Vamos calcular o trabalho realizado por ao longo desse deslocamento.
A força tem duas componentes, uma no eixo e outra no eixo :
Podemos calcular o trabalho de cada componente e depois somarmos:
Agora dá uma olhada no deslocamento:
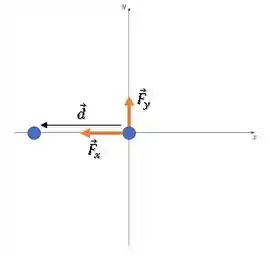
Para esse deslocamento ao longo do eixo , torna bem fácil o cálculo do trabalho, pois temos uma componente na mesma direção que o deslocamento e a outra perpendicular a ele.
Para a componente em :
O produto escalar entre dois vetores é dado pelo produto de seus módulos com o cosseno do ângulo entre eles:
Como o deslocamento está na mesma direção que a força, o ângulo entre eles é zero:
Enquanto o trabalho da componente em é:
Como eles são perpendiculares , então:
Assim, achamos que o trabalho da força é:
Resposta
Letra (D)