A figura mostra uma bola de massa rolando sem deslizamento numa trajetória espiral descendente no interior de um cone oco e numa região de campo gravitacional uniforme . O trabalho realizado pela força de contato da parede sobre a bola é:
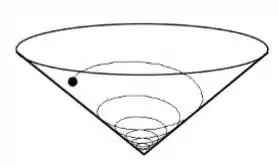
(a) zero.
(b) depende da aceleração gravitacional local e da massa da bola.
(c) depende da forma da trajetória espiral
(d) positivo.
(e) negativo.
Passo 1
A força de contato da parede sobre a bola, nada mais é que a força normal. Lembrando que o trabalho realizado é calculado a partir do produto escalar da força com a trajetória, em outras palavras, pela fórmula:
Onde é o ângulo entre a trajetória e a força. Quando esses dois fizerem 90° entre si, o trabalho realizado será nulo.
Passo 2
Em todos os casos a força normal é perpendicular a trajetória, vou te mostrar com algo mais básico, se liga nesse plano horizontal.
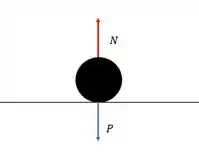
A força normal é perpendicular à trajetória portanto seu trabalho é:
No nosso caso vai acontecer o mesmo, independente desse plano estar inclinado ou não, se liga na figura:
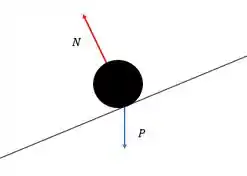
A força normal será sempre perpendicular a superfície, não importa como ela seja.
Então podemos afirmar com 100% de certeza que o trabalho realizado pela força normal na nossa espiral é:
Portanto, o trabalho da força de contato é nulo.
Resposta
Letra (a)