“Caminhando contra o vento
Sem lenço e sem documento
No sol de quase dezembro
Eu vou...”
Trecho da música “Alegria, Alegria” de Caetano Veloso que concorreu no III Festival da Record, em 1967 - um ícone do movimento Tropicalista.
Imaginemos o homem da canção com massa de e caminhando na direção de uma força de , a força do vento é de , o coeficiente de atrito é de . Os Trabalhos realizados por todas as forças que agem sobre o homem quando ele se descola em , são:
(a) e .
(b) e
(c) e .
(d) e .
(e) e .
Passo 1
Olá pessoas!!
Ele fala um monte de coisa nesse enunciado, mas fica difícil ver o que está acontecendo. Então vamos desenhar tudo! Acompanha aqui comigo.
Tem um homem andando (ele tem massa e ele sofre atração gravitacional, então tem Peso), se ele tá andando sobre o chão, então tem a Normal, e como essa superfície não é lisa, então tem Atrito no sentido oposto ao movimento. Ele tá andando em uma direção com uma força a favor do movimento, e temos contra o sentido do movimento a Força do vento.
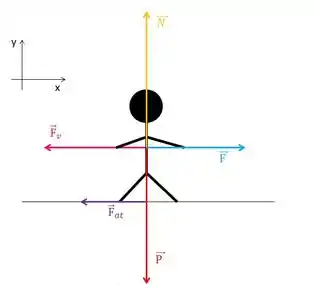
Notem que, colocamos os sentidos das forças como se ele estivesse andando para a direita, beleza?
Passo 2
Agora que a gente já viu o que tá acontecendo, vamos ver o que ele tá pedindo.
Eler quer que a gente calcule o trabalho de todas essas forças.
Lembrando que:
Esse é a distância percorrida, que o enunciado fala que foi . E o sentido dele é pra direita, já que é o sentido do movimento.
E o é o ângulo entre a força e o deslocamento.
Acompanha aqui:
Passo 3
Para a força
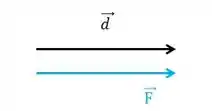
Então o ângulo é zero, e o cosseno é 1.
Beleza, vamos continuar.
Passo 4
Para a força do vento
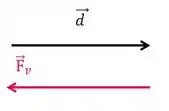
Então o ângulo é , e o cosseno é .
Show!!
Passo 5
Para a força de atrito
O módulo da normal é igual ao módulo do peso:
Então:
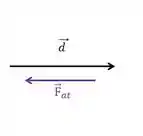
Então o ângulo é , e o cosseno é .
Uhuul! Menos uma! Falta pouco.
Passo 6
Para a força peso

Então o ângulo é , e o cosseno é .
Isso vai acontecer sempre que a força for perpendicular ao deslocamento, porque aí o cosseno zera
.
Qual outra força no nosso desenho é perpendicular ao deslocamento?
A normal! Então o trabalho dela também é zero
Então:
Olhando as alternativas, vemos que a letra E é a correta!

Resposta
Alternativa C.