UTFPR - Pato Branco - Física 1 - Listas - Teste 9 - Listas Prof. Marcelo Sandrini - Lista 4 - Questão 3
Um bloco de gelo escorrega para baixo em uma rampa sem atrito com inclinação de enquanto um operário o puxa (através de uma corda) com uma força paralela à rampa. Quando o bloco desliza uma distância ao longo da rampa, sua energia cinética aumenta de . Quão maior seria a energia cinética se o bloco não estivesse sendo puxado pela corda?
Passo 1
Oiie, tudo bem?
Aqui nós temos um problema de comparação entre duas situações! Primeiro, temos que um bloco desliza ao longo de um plano inclinado com inclinação , mas um operário está tentando segurar o bloco com uma força , mas ele não consegue segurar, e o bloco desliza por e ganha uma energia cinética . O esquema é o seguinte
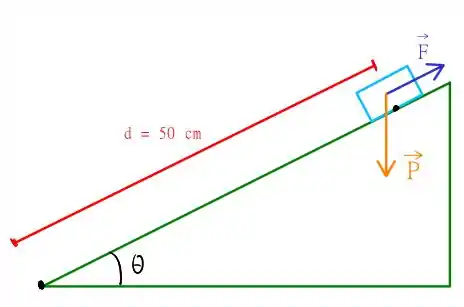
É pedido para que comparemos a energia no final desta rampa se a força não existisse! Sacou?
Para isso precisamos lembrar que como as forças que atuam neste sistema são todas conservativas, podemos dizer que a variação da energia cinética é equivalente ao trabalho realizado pelas forças! Ou seja
E como as forças são todas constantes, podemos escrever
em que é o ângulo entre a força e o deslocamento. Consegue partir daí? Se não, bora comigo!
Passo 2
Nós temos que o trabalho total realizado no sistema, é dado pela soma do trabalho da força peso mais o trabalho realizado pela força , . Vamos ignorar por enquanto o trabalho da força peso, já que ele é o mesmo em ambas as situações. Vamos calcular o trabalho , temos a seguinte expressão
No caso da força , a força é anti-paralela ao deslocamento (mesma direção mas sentido contrário), então , e temos que como e . Temos que
E agora, o que fazemos com isso? Dá uma olhada no passo 1, no que discutimos sobre a energia cinética do sistema. Bora lá!
Passo 3
Como temos que
Podemos obter que
E, como temos que , o trabalho realizado pela força peso é tal que
Interessante não é? Agora me diga, e se não existisse força ? Isso mudaria o peso que atua sobre o bloco? NÃO! Ou seja, mesmo que a força seja nula, temos que
Mas como isso é possível? Isso ocorre porque agora o bloco, sem ninguém segurando, vai ganhar mais energia cinética, ou seja, temos agora que
Ou seja, a energia cinética é maior por um fator de . A questão foi isso! Te vejo na próxima! Tchau Tchau!