Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Trabalho

Ver Teoria
Exercício 712345689101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

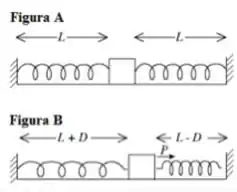
Duas molas idênticas, de constante elástica k = 200   N / m e comprimento relaxado 0,20 m , estão conectadas a um bloco, conforme ilustrado na figura A . Nesta configuração, as molas estão estendidas a um comprimento L = 0,30 m . Uma força externa P é capaz de arrastar o bloco para a direita, percorrendo uma distância D = 0,02 m , e mantê-lo nesta posição (ver figura B ). Calcule o trabalho realizado pela força externa sobre o bloco.

(A) 6,0   J  

(B) 0,060   J  

(C) 0,08   J  

(D) 12   J  

(E) 0,80   J

Passo 1

Temos que o trabalho feito por essa força se relaciona com o trabalho realizado pelas forças elásticas das duas molas

W P = - W 1 - W 2

Já que a força P se opões a essas forças.

Essa força P se relaciona com a variação de energia potencial das duas molas por

W P = Δ U 1 + Δ U 2

A variação de energia potencial da mola da esquerda é dada por

Δ U 1 = 1 2 k L + D - L 0 2 - 1 2 k L - L 0 2

Onde L 0 = 0,2 m é o comprimento relaxado da mola. Substituindo os valores temos

Δ U 1 = 1 2 200 0,3 + 0,02 - 0,2 2 - 1 2 200 0,3 - 0,2 2

Δ U 1 = 0,44 J

Já a variação de energia potencial da mola da direita é dada por

Δ U 2 = 1 2 k L - D - L 0 2 - 1 2 k L - L 0 2

Substituindo os valores temos

Δ U 2 = 1 2 200 0,3 - 0,02 - 0,2 2 - 1 2 200 0,3 - 0,2 2

Δ U 2 = - 0,36 J

Assim temos

W P = 0,44 - 0,36

W P = 0,08 J

Resposta

(C)

Exercícios de Livros Relacionados

Uma merendeira de 2,0k g escorrega em uma superfície sem atrito no sentido positivo de um eixo x . A partir do instante t = 0 , um vento constante aplica uma força à merendeira no sentido negativo do
Para puxar um engradado de 50k g sobre um piso horizontal sem atrito, um operário aplica uma força de 210N que faz um ângulo de 20 ° para cima com a horizontal. Em um deslocamento de 3,0m , qual é o t
Uma força F → = 4,0N i ^ + c j ^ age sobre uma partícula enquanto a partícula sofre um deslocamento d → = 3,0m i ^ - 2,0m j ^ . (Outras forças também agem sobre a partícula.) Qual é o valor de c se o
Uma força atuando sobre uma partícula de 2,0 kg do plano xy, nas coordenadas (x, y), é dada por F → = - b / r 3 x i ^ + y j ^ , onde b é uma constante positiva e r é a distância da partícula à origem.
Uma forca F → = 2,0N x 2 i ^ é aplicada sobre uma partícula inicialmente em repouso no plano xy. Encontre o trabalho realizado por esta força sobre a partícula e a rapidez final da partícula, quando e