UFABC – Fenômenos Mecânicos – Lista 4 – Questão 10
Uma corda é usada para puxar um bloco de com velocidade constante por ao longo de um piso horizontal. A força que a corda exerce sobre o bloco é de , dirigida acima da horizontal. Quais são
(a) o trabalho realizado pela força da corda,
(b) o aumento na energia térmica do sistema bloco-piso e
(c) o coeficiente de atrito cinético entre o bloco e o piso?
Passo 1
Oi galera, tudo bem? Essa questão é de aplicação das fórmulas de trabalho e do teorema trabalho-energia!
No problema temos um bloco de massa sendo puxado por uma corda com uma força . O pulo do gato é ver que como a velocidade com que o bloco se movimenta é constante, significa que há equilíbrio de forças nesse sistema!
Nesse bloco agem quatro forças: normal e peso na vertical e a força da corda (que tem componentes vertical e horizontal pois faz um ângulo de com a horizontal) e a força de atrito (puramente na horizontal, contrária ao movimento)
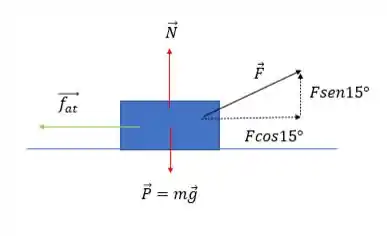
Como temos equilíbrio, a soma das forças na vertical, assim como na horizontal, é nula. E assim teremos duas equações para trabalharmos!
Mas relaxa, vou fazer junto com você!
Passo 2
Letra (a):
O trabalho de uma força é
No nosso caso e é o ângulo que a força faz com o vetor deslocamento. Aqui e , agora é só substituir:
Beleza? Aqui não tem mistério, é só aplicar a fórmula mesmo!
Passo 3
Letra (b): agora o problema pergunta o valor aumento da energia térmica do sistema bloco-solo
Como a velocidade do sistema é constante e não há forças externas, a energia dada pela força F em trabalho é dissipada pelo atrito
Então a energia que o atrito dissipa é numericamente igual ao trabalho realizado, mas com sinal negativo, pois há dissipação de energia:
Certo?
Passo 4
Letra (c): agora o problema pergunta o valor do coeficiente de atrito entre o bloco e o piso
Como sabemos a energia dissipada pelo atrito, vamos usar essa informação!
O trabalho da força de atrito é:
O deslocamento nós já sabemos, vale , mas agora o ângulo é diferente. O atrito SEMPRE atua no sentido contrário ao deslocamento, então
Beleza? E a força de atrito?
Passo 5
A força de atrito tem a ver com a normal:
E nesse caso a normal é igual a diferença entre a componente vertical da força F e o peso, vamos resgatar o desenho do passo 1:
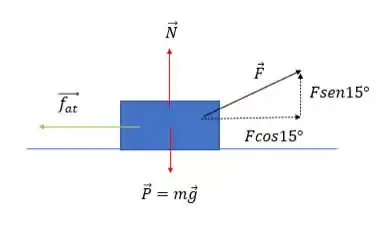
Como temos equilíbrio de forças:
Tranquilo ate aqui?
Passo 6
Agora com o valor da normal na mão, vamos voltar para o trabalho!
O trabalho realizado é , pois calculamos na letra (b)! agora é só substituir:
Beleza? Taí o coeficiente de atrito!
E é isso! Espero ter ajudado!