Um bloco de massa está sendo puxado ao longo de uma superfície com atrito. Se é a força externa que puxa o bloco, a força de atrito, a força peso, a força normal e a força resultante, todas elas atuando sobre o corpo, o trabalho de cada uma dessas forças, após o bloco deslocar-se por 2 metros a velocidade constante vale, respectivamente:

(A) , , , , ;

(B) , , , , ;

(C) , , , , ;

(D) , , , , ;

(E) , , , , ;

A força puxa o bloco ao longo da superfície, enquanto a força de atrito será contra o movimento.

Mas antes de desenharmos as forças, repara em uma coisa...

Ele não disse se a superfície tem uma inclinação ou é horizontal.

Porém, nesse caso, para qualquer inclinação, a força Normal sobre o bloco será perpendicular ao deslocamento:

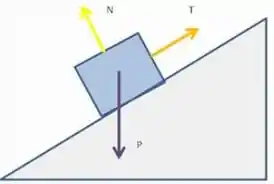
Assim, seu trabalho é zero sobre esse deslocamento:

Logo, já matamos que a resposta é a letra (A), pois é a única com o trabalho da força normal nulo.

Mas vamos dar uma olhada no trabalho das outras forças.

Assumindo que o plano é horizontal, temos as forças assim:

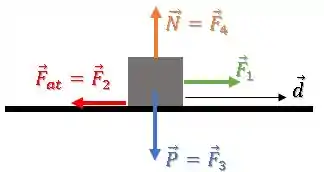
Sobre o trabalho da força peso , podemos pensar que não há variação de altura ou então que a força está perpendicular ao movimento.

As duas justificativas são equivalentes e mostram que:

Já a força está na mesma direção e sentido do deslocamento, portanto seu trabalho será:

Por último vamos à força de atrito .

Como o bloco está em equilíbrio, temos que:

Ou seja, a força de atrito tem o mesmo módulo da força que puxa o bloco, mas com o sentido oposto.

Como ela está na mesma direção do deslocamento mas com sentido contrário, seu trabalho é negativo e pode ser calculado com:

Então confirmamos que a resposta realmente é a letra (A).

OBS: Aquela massa de do enunciado não serve pra nada, é só pra confundir o pessoal mesmo haha.