USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 54a
Uma partícula move-se, sob a ação da força , no plano . Calcule:
a) O trabalho realizado pela força ao longo do quadrado indicado na figura . O que você conclui sobre o caráter conservativo ou não de ?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma força , que realiza um trabalho ao longo do quadrado indicado na figura abaixo:
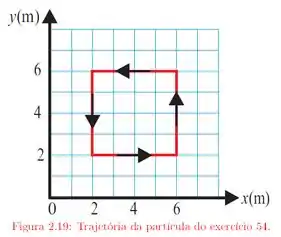
Nós precisamos determinar o valor desse trabalho e verificar se a força é conservativa. Lembrando que o trabalho é calculado por:
E que para a força ser conservativa, o trabalho precisa ser independente da trajetória, então, o trabalho total calculado ao longo do caminho precisaria ser zero. Vamos verificar isso!
Passo 2
Galera, vamos começar dividindo o quadrado em partes. Assim, teremos:
Então, o trabalho total vai ser a soma dos trabalhos calculados em cada caminho, ou seja:
E como , vamos calcular as integrais nos intervalos respectivos de .
Começando com , para e , temos:
Uma coisa importante que nós vamos usar, é o produto vetorial entre os versores e . Onde:
Assim, vamos ter:
Integrando e considerando os pontos onde começa (no caso, em ) e termina (no caso, em ), temos:
Passo 3
Vamos fazer o mesmo para :
Integrando e aplicando os intervalos, temos:
Para , de maneira análoga, temos:
Integrando e aplicando os intervalos:
E por fim, para :
Integrando e aplicando os intervalos:
Passo 4
Somando , , e , temos o trabalho total:
Como ao longo do caminho fechado, ele depende do caminho e, portanto, a força não é conservativa.
Valeu, galera! Até a próxima! 😉