Um bloco de massa é deslocado para cima por uma força uma distância ao longo de um plano inclinado. O plano está inclinado de em relação à horizontal, e a força faz um ângulo com a vertical. Determine o trabalho realizado pela força ao longo do deslocamento. Utilize o sistema de coordenadas indicado na figura.
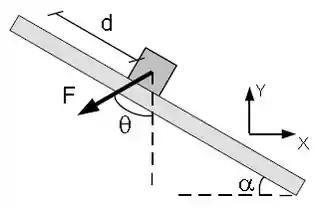
Passo 1
Decompor a força
Pra calcular o trabalho, precisamos de informações da força e do deslocamento, certo? Dá uma olhada na força, primeiro, como ela fica quando decomposta:
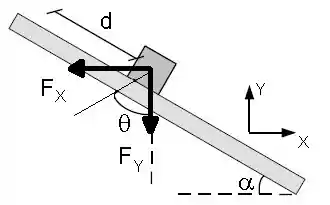
Podemos escrever então a força da seguinte forma galera:
Passo 2
Decompor o deslocamento
Como já temos informações da força, falta pra gente só decompor o vetor deslocamento para obtermos informações do mesmo. O vetor deslocamento decomposto fica:
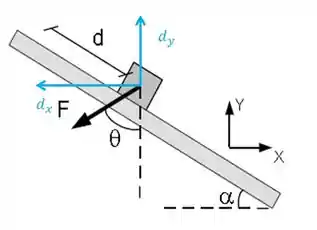
Podemos escrever então o deslocamento da seguinte forma galera:
Passo 3
Calcular o trabalho
Agora pra calcular o trabalho basta a gente aplicar a fórmula! Vamos lá: