Um guindaste ergue verticalmente um caixote a uma altura de em . Um segundo guindaste ergue o mesmo caixote à mesma altura em . Em ambos os casos o içamento foi feito com velocidade constante. O trabalho realizado pelo primeiro guindaste, comparado com o trabalho realizado pelo segundo, é
(a) quatro vezes maior
(b) igual à metade.
(c) duas vezes maior.
(d) o mesmo
(e) quatro vezes menos
Passo 1
Fala aí!!!
Vamos entender essa situação que ele fala pra gente.
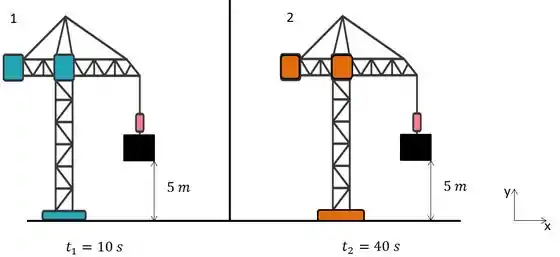
Então, a única coisa que muda de um guindaste para o outro é o tempo que demorou para eles levantarem o bloco.
A pergunta é sobre o trabalho que os guindastes fazem pra levantar o bloco. Mas, e aí, o tempo de levantamento influencia no trabalho do guindaste?
Vamos pensar nisso juntos! Acompanha aqui comigo.
Passo 2
Pra gente calcular o trabalho de uma força , usamos a relação:
Onde é o deslocamento e é o ângulo entre o deslocamento e a força.
No nosso caso, o deslocamento é de 5 metros, e a força é a tração que o fio do guindaste faz.
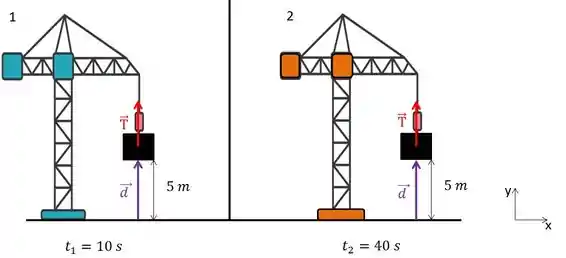
Note que a força e o deslocamento apontam na mesma direção, então o ângulo entre eles é zero, logo
Calculando os trabalhos da tração do guindaste em ambos os casos:
Logo os trabalhos são iguais!!
O trabalho não é uma grandeza que depende do tempo!
Resposta
Alternativa (d)