UTFPR - Pato Branco - Física 1 - Listas - Teste 9 - Listas Prof. Marcelo Sandrini - Lista 4 - Questão 1
Uma moeda desliza sobre um plano sem atrito em um sistema de coordenadas , da origem até o ponto de coordenadas , sob o efeito de uma força constante. A força tem um módulo de e faz um ângulo de no sentido anti-horário com o semi-eixo positivo. Qual é o trabalho realizado pela força sobre a moeda durante esse deslocamento?
Passo 1
Oiie, tudo bem?
O enunciado nos diz que uma moeda desliza em um plano sem atrito, da origem até o ponto de coordenadas , sob efeito de uma força constante em uma direção específica. A direção da força é dada pelo seguinte ângulo com o eixo no sentido anti-horário , temos o seguinte esquema de todo este sistema
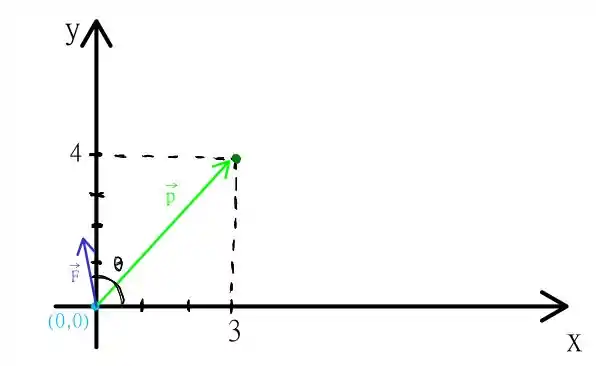
A questão pede então que calculemos o trabalho realizado por esta força, para levar a partícula da origem até o ponto . Como podemos fazer isso? Como aqui temos um caminho retilíneo e uma força constante, podemos simplesmente utilizar que
em que é o vetor deslocamento, e é o ângulo entre o vetor deslocamento e a força aplicada. Sabe quem é este vetor em nosso caso? Como temos que partimos da origem, . Já que um vetor deslocamento pode ser obtido calculando a diferença entre o ponto final e inicial. Vamos aplicar então a expressão para o trabalho! Vem comigo!
Passo 2
Para utilizar a fórmula para o trabalho precisamos saber qual é o ângulo . Olhando o esquema do passo 1, sabe dizer qual será este ângulo? Saca só! Temos que de acordo com nosso enunciado, mas vamos analisar o seguinte esquema
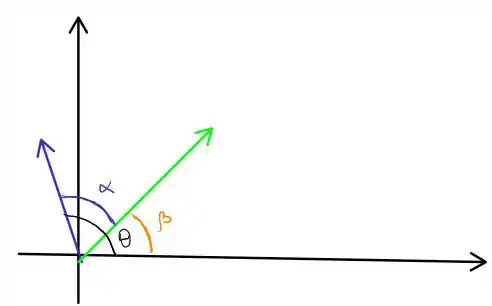
No que temos . Nós precisamos saber quem é , mas para isso, precisamos de . Consegue pensar em alguma maneira de obter este ângulo? Eu sugiro montar o seguinte triângulo retângulo:
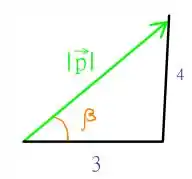
Se lembra das relações de seno, cosseno e tangente de um triângulo retângulo? Nós temos aqui dado para nós o cateto oposto e o adjacente, então, podemos dizer que
E, portanto podemos dizer que , ou podemos lembrar que equivale ao ângulo de para utilizar a regra de e obter
Maravilha! Com isso podemos calcular qual é o ângulo e o trabalho que a força realizou! Bora lá!
Passo 3
Se temos que , podemos calcular que
E, portanto, temos que . E então o trabalho pode ser obtido como
O módulo da força nos é dado no enunciado como , mas você lembra como obter o módulo do vetor ? Precisamos utilizar a seguinte relação
em que e são respectivamente os componentes de em e . Fazendo a continha acima temos . E, portanto, temos que
que resulta em
A questão foi isso! Te vejo na próxima! Tchauzinho!