Um corpo de está em repouso sobre uma superfície horizontal, sem atrito. Uma força de módulo constante de , fazendo um ângulo de 30◦ com a horizontal, puxa o corpo. Determinar o trabalho efetuado pela força da corda e a velocidade escalar final do corpo, depois de deslocar-se sobre a superfície horizontal.

Fala, galera! Vamos resolver essa questão!

O enunciado nos deu um corpo de massa que tava em repouso inicialmente, mas acaba sendo puxado por uma força , que faz um ângulo com a horizontal, e percorre uma distância . Seria mais ou menos isso aqui:

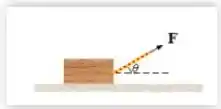
Para calcular o trabalho que essa força exerce no corpo, nós precisamos lembrar que o trabalho é igual ao produto da força pela distância e pelo cosseno do ângulo, ou seja:

Já para calcular a velocidade final do corpo, vamos lembrar do teorema do trabalho e energia cinética, que diz que o trabalho é igual a variação da energia cinética. A energia cinética é dada por , então ela varia conforme a equação , onde é a velocidade final e é a velocidade inicial. Mas, como ele tava inicialmente parado, nossa velocidade inicial é nula, . Assim, pelo teorema do trabalho e energia cinética, vamos ter:

Isolando , vamos encontrar nossa velocidade final. Vamos lá!