Considerando o trabalho realizado por uma força , entre a origem e o ponto ao longo dos caminhos:
- Primeiro ao longe de e depois ao longo de
- Primeiro ao longo de e depois ao longo de
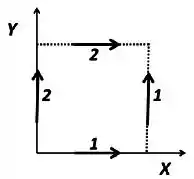
Podemos afirmar que:
Passo 1
Vamos começar usando que a gente já sabe de trabalho, fechou ?
Ou seja, a força e o deslocamento precisam ser paralelos ou antiparalelos pra ter algum valor em módulo, certo? Só com essa informação descobrimos que os trabalhos que estão subindo são nulos, pois são perpendiculares ao eixo .
E as outras duas partes ?
Passo 2
Como a força tem componente , se o for zero a força é nula e assim não tem trabalho, ou seja, só vai ter trabalho na parte superior da parte 2 e não vai ter trabalho na parte inferior da parte 1.
Resposta
Exercícios de Livros Relacionados
Uma merendeira de 2,0k g escorrega em uma superfície sem atrito no sentido positivo de um eixo x . A partir do instante t = 0 , um vento constante aplica uma força à merendeira no sentido negativo do
Para puxar um engradado de 50k g sobre um piso horizontal sem atrito, um operário aplica uma força de 210N que faz um ângulo de 20 ° para cima com a horizontal. Em um deslocamento de 3,0m , qual é o t
Uma força F → = 4,0N i ^ + c j ^ age sobre uma partícula enquanto a partícula sofre um deslocamento d → = 3,0m i ^ - 2,0m j ^ . (Outras forças também agem sobre a partícula.) Qual é o valor de c se o
Uma força atuando sobre uma partícula de 2,0 kg do plano xy, nas coordenadas (x, y), é dada por F → = - b / r 3 x i ^ + y j ^ , onde b é uma constante positiva e r é a distância da partícula à origem.
Uma forca F → = 2,0N x 2 i ^ é aplicada sobre uma partícula inicialmente em repouso no plano xy. Encontre o trabalho realizado por esta força sobre a partícula e a rapidez final da partícula, quando e