UFPE – Física 1 2019.2 – Prova Final– Questão 4
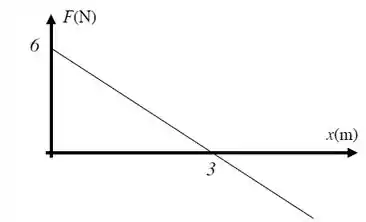
Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força , com em metros e em newtons. Inicialmente a partícula encontra-se na posição com velocidade inicial . Qual é a velocidade ao passar pela posição ?
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Para resolver essa questão vou usar o teorema trabalho-energia. Esse teorema nos diz que todo trabalho realizado pela força resultante sobre um corpo é igual à variação de energia cinética que esse corpo vai experimentar.
Os dados que o problema nos dá são:
E queremos saber a velocidade quando temos . Então a ideia aqui é a seguinte: achar o trabalho realizado no deslocamento de até , integrando a força em relação ao deslocamento. Depois usar esse valor para, junto com a variação da energia cinética, achar a velocidade final. Vamos começar?
Passo 2
Primeiro o trabalho realizado:
Passo 3
A partir disso, vamos usar o teorema. O trabalho realizado vai ser igual à variação de energia cinética:
A massa é , a velocidade inicial vale e o trabalho é . Agora é só substituir ali em cima e achar :
A alternativa certa é a (e).
Beleza?
Pronto pra próxima questão? =)
Resposta
Alternativa (e).