UTFPR - Pato Branco - Física 1 - Listas - Teste 9 - Listas Prof. Marcelo Sandrini - Lista 4 - Questão 6
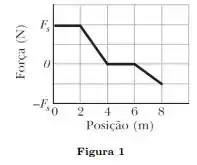
Um bloco de massa se move em uma linha reta sobre uma superfície horizontal sem atrito sob a influência de uma força que varia com a posição, como mostra a Fig. 1. A escala vertical do gráfico é definida por . Qual é o trabalho realizado pela força enquanto o bloco se desloca da origem até ?
Passo 1
Oiie, tudo bem?
Nós temos aqui um bloquinho com massa que se move em linha reta, no entanto, a força varia com a posição que o bloquinho se encontra. O gráfico nos dá exatamente a forma com que a força varia com a posição
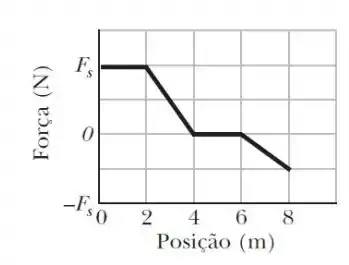
Note que nos é dado que , e o eixo horizontal indica a posição. Nós vamos precisar justificar a expressão utilizada para calcular o trabalho em diferentes regiões do gráfico observando a forma como a força evoluí. Note que em alguns momentos ela é constante e em outros ela cai com uma certa inclinação. Vamos fazer passo a passo! Vem comigo!
Passo 2
O primeiro trecho é bastante direto, note que no intervalo até , temos uma reta horizontal, e portanto, uma força constante, o trabalho pode ser calculado neste deslocamento como
Ou, seja, temos que . Temos também outro intervalo em que a força é constante, o intervalo de até , no entanto, temos que a reta constante está em , portanto
Vamos analisar agora os intervalos em que a força não é constante! Vem comigo!
Passo 3
No intervalo de até temos o seguinte triângulo
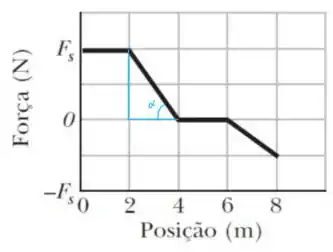
Nós temos que é uma reta de inclinação negativa. A equação da reta seria da forma
Temos que quando , , portanto, podemos dizer que
Também temos que em , , portanto, temos que
Desta última equação encontramos que , ou seja, temos da primeira equação que
De forma que e . E a nossa força obedece a seguinte relação relação
Okay! Sabemos como a força evolui! Mas e daí? Não podemos calcular o trabalho da forma que calculamos na primeira parte! Agora, precisaremos utilizar uma relação um pouco mais geral! Você consegue se lembrar? Saca só!
Passo 4
Temos que o trabalho realizado por uma força ao longo de uma trajetória é dado por
Usando em nosso caso, que estamos no intervalo e e e a força que obtivemos no passo anterior, temos que
Lembrando que estas integrais tomam a seguinte forma
e, também que
Calculando o valor explicitamente, temos que
Ou seja, o trabalho realizado neste intervalo é
Falta apenas um intervalo para calcularmos! Este intervalo é bastante parecido com o que fizemos agora! O processo é o mesmo! Então, vamos repeti-lo! Vem comigo!
Passo 5
No intervalo de até temos o seguinte triângulo
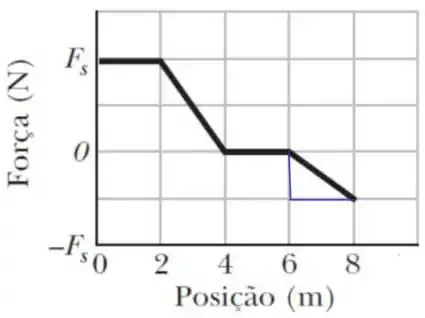
Nós temos que é uma reta de inclinação negativa. A equação da reta seria da forma
Temos que quando , , portanto, podemos dizer que
daqui temos que . Também temos que em , , portanto, temos que
Ou seja, temos que
De forma que e portanto . A equação fica então da forma
Vamos agora aplicar novamente a integral para o cálculo do trabalho! Vem comigo!
Passo 6
Como estamos no intervalo até
Lembrando que estas integrais tomam a seguinte forma
e, também que
Calculando o valor explicitamente, temos que
Ou seja, o trabalho realizado neste intervalo é
Agora é só somar todo mundo! Temos que
Finalmente, temos que o trabalho é . A questão é isso! Te vejo na próxima! Tchau Tchau!