Uma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .

d) Determine o trabalho realizado pela força para deslocar o corpo desde até ;

Fala, galera! Vamos resolver essa questão!

O enunciado nos deu uma partícula de massa , que se move na direção por meio da força . A partir disso, temos o gráfico de :

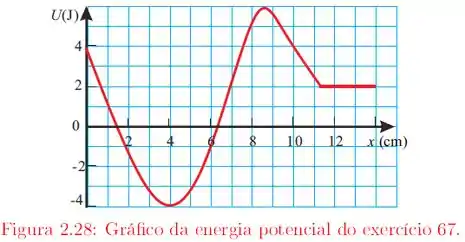
Precisamos determinar o trabalho realizado pela força para deslocar o corpo desde até . Para isso, vamos usar o teorema do trabalho e energia potencial, que nos diz que o trabalho é o negativo da variação de energia potencial, ou seja:

Assim, verificando os valores de para e para , calculamos a variação de energia potencial e obtemos o trabalho realizado no intervalo.

Vamos lá!