Halliday - Vol.1 - Ed. 8 - Capítulo 7 – Problemas Adicionais – Questão 56
(Capítulo 7 – Problemas Adicionais - Exercício 56) Para puxar um engradado de sobre um piso horizontal sem atrito, um operário aplica uma força de que faz um ângulo de para cima com a horizontal. Em um deslocamento de , qual é o trabalho realizado sobre o engradado (a) pela força do operário, (b) pela força gravitacional e (c) pela força normal do piso? (d) Qual é o trabalho total realizado sobre o engradado?
Passo 1
Oi, galerinha! Tudo bom? Nessa questão devemos perceber que somente três forças agem sobre a caixa, a força do operário, a força peso e a força normal.
Como todas elas são forças constantes, podemos usar a seguinte relação para calcular o trabalho:
Lembrando que para determinar o trabalho total, podemos usar essa fórmula individualmente para cada força e depois somar todos os trabalhos.
Passo 2
a) Para determinar o trabalho da força que o operário faz sobre caixa, usaremos a :
Passo 3
b-c) Bora resolver a b e c juntas! Repara que como o deslocamento ocorre na horizontal e, a força normal e o peso agem na vertical, elas são perpendiculares ao deslocamento.
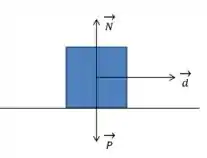
Portanto, o ângulo entre elas e o deslocamento é e o cosseno de é nulo. Assim:
Passo 4
d) Com o trabalho realizado por cada força calculado, podemos determinar o trabalho total:
Resposta
- ;
- ;
- ;
- .