Trabalho e Energia Cinética
A figura mostra dois caminhos ( e ) ao longo dos quais uma partícula é levada da origem até o ponto . Nessa região há uma força . Pode-se dizer do trabalho realizado por :
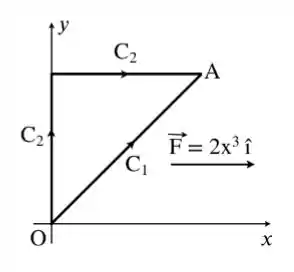
(a) que depende da massa da partícula.
(b) que é maior ao longo do caminho .
(c) que ao longo de e são iguais numericamente à área do triângulo delimitado pelos 2 caminhos.
(d) que é igual para os dois caminhos.
(e) que é maior ao longo do caminho .
Passo 1
Primeiramente, precisamos entender o que significa aquela expressão da força:
Ela nos diz que:
- A força vai estar sempre na direção do eixo
- O seu módulo só varia com a mudança na coordenada .
Passo 2
Portanto, para facilitar, vamos abrir o caminho inclinado em duas partes, para isso, fazemos as componentes horizontal e vertical dele, como na figura abaixo.
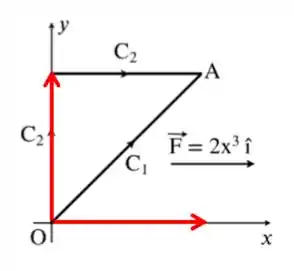
Passo 3
Temos então segmentos para analisar: , vamos um por um, supondo que a distância entre o eixo e o ponto é :
-
Utilizando a fórmula do trabalho, temos que:
Como o deslocamento e a força estão na mesma direção, e , logo:
-
O pensamento é o mesmo do caminho anterior, já que o deslocamento em é o mesmo.
-
Utilizando a fórmula do trabalho, temos que:
Como o deslocamento e a força estão em direções perpendiculares, , logo, pela característica do produto escalar:
-
Mesmo pensamento do anterior:
Passo 4
Portanto, temos que:
Logo:
Resposta
Letra (d)