Um objeto preso a um fio ideal descreve uma trajetória circular num plano horizontal com rapidez constante. O trabalho realizado pela tensão é nulo porque
(A) O deslocamento para cada revolução é nulo.
(B) A tensão média para cada revolução é nula.
(C) A velocidade é constante.
(D) A magnitude da aceleração é nula.
(E) A tensão é perpendicular a cada deslocamento infinitesimal.
Passo 1
Dá uma olhada no que está acontecendo:

À todo instante o fio está exercendo uma força de tração que aponta para o centro da trajetória circular.
Lembra da fórmula de trabalho?
É o produto escalar entra a força e o deslocamento:
O produto escalar pode ser escrito da seguinte forma:
Onde o ângulo é o ângulo entre o vetor da força e o vetor do deslocamento.
E como achamos esse ângulo?
Primeiro, a força de tração ela sempre aponta para o centro, então ela atua como uma força centrípeta.
Segundo, como a direção do deslocamento muda a todo instante, vamos considerar um intervalo de tempo muito pequeno, onde haverá uma deslocamento muito pequeno na direção da velocidade. Como a velocidade é sempre tangencial ao círculo, temos:
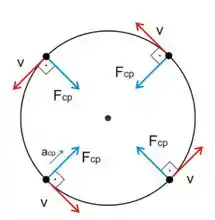
Repara que em qualquer instante a força de tração (centrípeta) e o deslocamento (direção da velocidade) fazem . Portanto, o trabalho dessa força será:
Como :
Assim, a justificativa para esse trabalho ser nulo é que a Tensão é sempre perpendicular a cada deslocamento pequenininho que chamamos de infinitesimal.
Sempre que uma força for perpendicular ao deslocamento, seu trabalho será nulo.
Resposta
Letra (E)