Uma bola é obrigada a seguir uma trajetória circular devido a uma força conservativa. Durante um intervalo de tempo , a bola realiza exatamente uma revolução. Qual das seguintes afirmações sobre o trabalho durante o tempo é verdadeira?
A. O trabalho é maior do que zero;
B. O trabalho depende apenas do raio da circunferência;
C. O trabalho depende apenas da velocidade da bola;
D. O trabalho depende apenas do tempo;
E. O trabalho é igual a zero;
Passo 1
Vamos destacar alguns pontos importantes do enunciado:
“trajetória circular”Isso quer dizer que o ponto inicial da trajetória é igual ao ponto final;
“força conservativa”Essas sao as nossas forças “especiais”. O trabalho delas só depende da posição inicial e da posição final;
“uma revolução” Uma volta completa em um círculo significa que você voltou para a mesma posição de que você tinha saído.
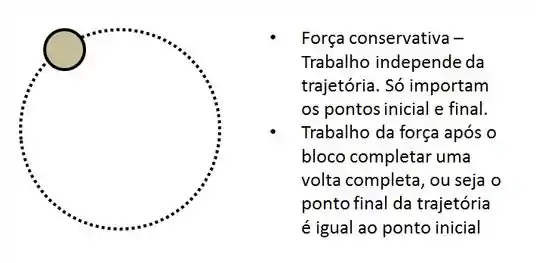
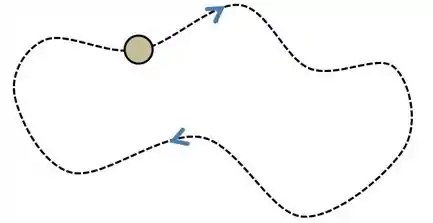
Em relação a uma força conservativa, se a posição inicial é igual a posição final então o trabalho é nulo. Não importa se é uma trajetória circular ou não, o importante é a posição inicial seja igual a final, aí o trabalho da força vai ser zero!
Passo 2
Vamos analisar as alternativas:
A. O trabalho é maior do que zero; Não! Se as posições inicial e final são iguais, o trabalho é zero!
Passo 3
B. O trabalho depende apenas do raio da circunferência;
C. O trabalho depende apenas da velocidade da bola;
D. O trabalho depende apenas do tempo;
Não! A dependência é com as posições inicial e final.
Passo 4
E. O trabalho é igual a zero;
Show! Essa é a correta!
Resposta
Alternativa E.