Um disco com momento de inércia de e raio de 0,25 gira em torno de um eixo fixo perpendicular ao disco e passando pelo seu centro. Uma força de 2,0 N é aplicada tangencialmente à borda do disco. Até o disco completar meia volta, o trabalho feito pela força é aproximadamente:
a) 10 J
b) 1,6 J
c) 40 J
d) 2,5 J
e) 6,3 J
Passo 1
Temos uma força que atua tangencialmente à borda de um disco:
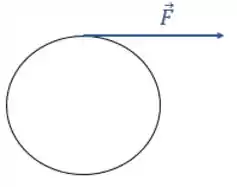
Lembramos agora, que o trabalho de uma força é igual a:
Onde d é o deslocamento linear da extremidade do disco aonde está atuando a força F, e esse deslocamento é tangente ao círculo, assim como a força, logo
Dessa forma,
Resposta
Letra b)
Exercícios de Livros Relacionados
Uma merendeira de 2,0k g escorrega em uma superfície sem atrito no sentido positivo de um eixo x . A partir do instante t = 0 , um vento constante aplica uma força à merendeira no sentido negativo do
Para puxar um engradado de 50k g sobre um piso horizontal sem atrito, um operário aplica uma força de 210N que faz um ângulo de 20 ° para cima com a horizontal. Em um deslocamento de 3,0m , qual é o t
Uma força F → = 4,0N i ^ + c j ^ age sobre uma partícula enquanto a partícula sofre um deslocamento d → = 3,0m i ^ - 2,0m j ^ . (Outras forças também agem sobre a partícula.) Qual é o valor de c se o
Uma força atuando sobre uma partícula de 2,0 kg do plano xy, nas coordenadas (x, y), é dada por F → = - b / r 3 x i ^ + y j ^ , onde b é uma constante positiva e r é a distância da partícula à origem.
Uma forca F → = 2,0N x 2 i ^ é aplicada sobre uma partícula inicialmente em repouso no plano xy. Encontre o trabalho realizado por esta força sobre a partícula e a rapidez final da partícula, quando e