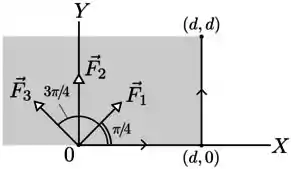
Uma partícula move-se no plano em uma trajetória retilínea ao longo do eixo , da origem ao ponto , e a seguir ao longo de uma trajetória retilinea do ponto ao ponto , como indicado na figura. Durante todo o percurso agem sobre a partícula três forças constantes , e de mesmo módulo. Os ângulos que as forças , e fazem com o eixo são, respectivamente, , e . Denotando os respectivos trabalhos das três forças em todo o percurso de a por , e , podemos afirmar que
- , e ;
- , e ;
- , e ;
- , e ;
- O trabalho realizado por cada uma das três forças é o mesmo.
Passo 1
Podemos perceber que é na direção do deslocamento, já que ele sobe e vai para a direita, o ângulo que esse deslocamento final faz é que é .
Além disso, a força é perpendicular ao movimento, porque
Podemos perceber também que o ângulo da força com o deslocamento é
Passo 2
Podemos achar então o trabalho de cada força, como nas alternativas ele não se interessa pelo valor, mas sim em comparar os trabalhos de cada força, vamos chamar de a distancia que eles percorrem, não precisamos perder tempo calculando essa distancia.
Além disso, vamos chamar o módulo de todas as forças de , já que são iguais
Então
Temos que
Resposta
Letra C