Questão 1). Um corpo de massa é arrastado horizontalmente para a direita por uma força constante , que faz um ângulo acima da superfície . O corpo parte do repouso e após percorrer uma distância , o módulo de sua velocidade é . Há atrito entre o corpo e a superfície. Considere a aceleração da gravidade local. Com base nos conceitos de Energia e Trabalho (conteúdos estudados nos cap. 4, 5 e 6), determine, em função dos dados que se fizerem necessários (, , , , e )

a) o trabalho realizado sobre o corpo pela força .

b) o trabalho total realizado sobre o corpo.

c) o trabalho realizado sobre o corpo pela força de atrito cinético.

d) o coeficiente de atrito cinético entre o corpo e a superfície.

Supondo que nosso sistema é exemplificado pela figura abaixo, vamos montar nossas respostas.

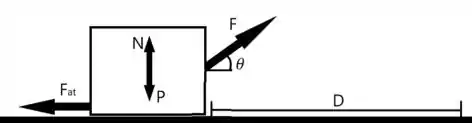
Primeiro vamos analisar o trabalho realizado pela força .

O trabalho realizado por uma força é dado pela distância percorrida multiplicada pela componente da força na direção do movimento, no caso .

A componente da força é dada por , concorda?

Então o trabalho realizado pela força será

Entendeu o porquê? 👀

Vamos pular uma pergunta e responder qual é o trabalho realizado pela força de atrito.

A força de atrito é obtida por

A normal é a força que se contrapõe a força peso , porém como exerce uma força a um ângulo , pode contribuir para a diminuição da força .

A componente de aponta para cima e podemos chama-la de .

Com isso, se no eixo há um equilíbrio de forças, a formal é dada por

Sabemos que a força peso é dada pelo produto entre a massa e a aceleração gravitacional .

Substituindo em , temos

Se o trabalho é a força multiplicada pelo deslocamento e no caso elas estão em sentidos opostos, podemos dizer que

Organizando a resposta, vamos obter que o trabalho realizado pela força de atrito é

Tranquilo até aqui? 😎

Assim podemos obter facilmente o trabalho realizado sobre o corpo pois como em não há movimento o trabalho é realizado pelas forças horizontais que calculamos.

Portanto o trabalho realizado é dado pelo trabalho da força somado ao trabalho da força de atrito.

Substituindo e pelos seus respectivos resultados que obtivemos anteriormente, chegamos em

Simplificando o resultado, temos

Entendeu essa parte? 😁

Por fim, queremos obter o coeficiente de atrito entre a superfície e o corpo.

Anteriormente chegamos à conclusão que a força de atrito é dada por

Se isolarmos em um lado da equação, vamos obter o coeficiente

Com isso obtermos o valor do coeficiente de atrito cinético!

Entendeu tudo? 😉

Fim! Iae, o que achou? Responde Aí! 😁