Questão discursiva – UFTPR – Campo Mourão – Física 1 – Lista de exercícios VII – questão 3c
Um trenó e seu ocupante, com uma massa total de , descem uma encosta e atingem
um trecho horizontal retilíneo com uma velocidade inicial de . Se uma força desacelera o trenó até o repouso a uma taxa constante de
c) Qual o trabalho realizado pela força sobre o trenó?
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
O centro de toda questão era calcularmos o trabalho realizado pela força . Como sabemos isso? Porque para que calculemos o trabalho realizado pra uma força sobre um caminho, precisamos da força e do caminho, que foi o que achamos no item a) e b). Mas como é o trabalho então?
A nossa força atua na direção horizontal, logo o nosso caminho é sobre o eixo também. Assim:
Se a força for constante em todo o percurso, ela não depende do caminho, logo:
O caminho nós já achamos, que é . Portanto:
Aplicando o produto escalar:
Sendo o ângulo formado entre a força e o caminho.
Então vamos achar e achar o nosso trabalho?
PS: lembre-se que nos itens anteriores achamos e
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Para sabermos o ângulo precisamos fazer um diagrama de forças do trenó. Assim:
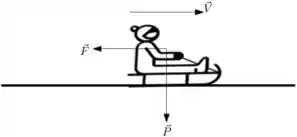
Onde é a força peso, é nossa força e que não é força, mas sim indica a direção da velocidade do trenó.
Então nós podemos ver o caminho aponta para um lado (direito) e a força para o outro (esquerdo), certo? Então concorda comigo que o ângulo formado entre eles é de ? Ok, vamos lá.
Agora vamos substituir os valores e partir pro abraço
Passo 3
Logo temos:
Ou melhor:
Então descobrimos que o trabalho que a força realizou sobre o trenó é de
E terminamos por aqui. Camarada. Obrigado por ter vindo até aqui comigo. Até a próxima!