UFABC – Fenômenos Mecânicos – Lista 4 – Questão 04
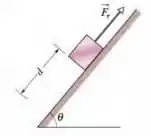
Na figura, um bloco de gelo escorrega para baixo em uma rampa sem atrito com uma inclinação enquanto um operário puxa o bloco (através de uma corda) com uma força, que tem um módulo de e aponta para cima ao longo da rampa. Quando o bloco desliza uma distância ao longo da rampa, sua energia cinética aumenta . Quão maior seria a energia cinética se o bloco não estivesse sendo puxado por uma corda?
Passo 1
Oi, pessoal, tudo bem? Aqui temos um bloco de gelo sendo puxado por um operário, mesmo assim ele cai e desliza por uma distância ao longo da rampa, aumentando sua energia cinética.
Vamos pensar juntos: se não houvesse essa força, ele aumentaria a energia cinética, certo? E aumentaria quanto? O quanto a corda ‘tirou’ de energia dele!
Assim, achando a contribuição da corda, sabemos o quanto de energia iria aumentar!
Passo 2
Então pessoal, nós sabemos que podemos achar a contribuição da corda através da relação:
Como a direção da força da corda é a mesma do movimento do bloco, porém possui sentido diferente, o ângulo entre a força e o deslocamento é:
Sendo assim:
Dessa forma, a energia cinética aumentaria se o bloco não estivesse preso a uma corda e sofresse o mesmo deslocamento.
E é isso! Espero ter ajudado!