Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Concavidade

Ver Teoria
Exercício 4812345678910111213141516171819202122232425262728293031323334353637383940414243444546474950515253545556575859606162636465666768697071727374

Enunciado

UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 29iiif

Considere em cada um dos itens abaixo a função dada por g ( x ) e em seguida determine o que

se pede:

g ( x ) = 2 x x 2 - 4

Determine os intervalos para os quais o gráfico de g ( x ) é côncavo para cima ou para baixo.

Passo 1

Fala galera, tudo beleza? Vamos para mais uma questão de cálculo . Nosso objetivo é obter os pontos de inflexão do gráfico.

Mas o que são pontos de inflexão mesmo? Bem, por definição, esses são os pontos onde temos uma mudança na concavidade do gráfico. Ou seja, se p for ponto de inflexão, então a concavidade do gráfico antes de p é diferente da concavidade do gráfico depois de p .

Agora, como podemos obter informação sobre a concavidade de um gráfico?

Usamos a segunda derivada!!!! O sinal da segunda derivada indica a concavidade de uma função. Se for positivo, a concavidade é para cima, e se for negativo, para baixo.

Ou seja, podemos inferir que os pontos de inflexão ocorrem quando há mudança de sinal na segunda derivada da função. Então vamos começar derivando a nossa g ( x ) . Lembrando que

g ( x ) = 2 x x 2 - 4

Mas já calculamos a primeira derivada de g . Ela era

d d x g ( x ) = - 2 ( x 2 + 4 ) / ( x 2 - 4 ) 2

Vamos calcular a sua segunda derivada

d 2 d x 2 g ( x ) = d d x d d x g ( x )

= d d x - 2 ( x 2 + 4 ) / ( x 2 - 4 ) 2

Usando a regra da razão da derivada, temos

d d x - 2 ( x 2 + 4 ) / ( x 2 - 4 ) 2 = ( 4   x   ( 12   +   x 2 ) ) / ( - 4   +   x 2 ) 3

Passo 2

Agora, vamos verificar os sinal do numerador da nossa segunda derivada

4   x   ( 12   +   x 2 )

Se já podemos observar que x = 0 é raiz do numerador, e além disso, temos que

4   x   ( 12   +   x 2 ) > 0   s e   x > 0

4   x   ( 12   +   x 2 ) < 0   s e   x < 0

Representando na reta real, os sinais do numerador ficam:

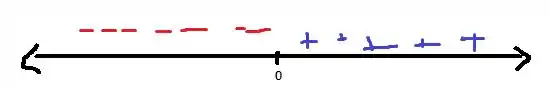
Agora vamos olhar o denominador

( - 4   +   x 2 ) 3

quando esse cara é positivo? Quando

- 4   +   x 2 > 0

⇒ 2 < x     o u   x < - 2

E quando é negativo?

- 4   +   x 2 < 0

⇒ - 2 < x < 2

Representando na reta real, os sinais do denominador ficam:

Então, fazendo o estudo do sinal da fração obtemos

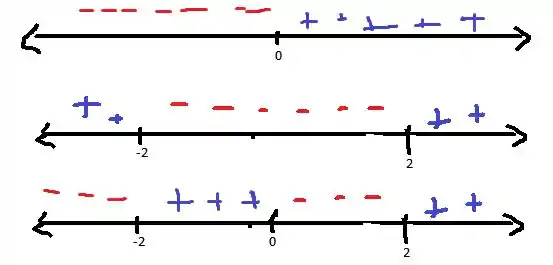
Dessa forma, as concavidades da nossa função g são:

P a r a   c i m a   s e   - 2 < x < 0   e   x > 2

P a r a   b a i x o   s e   x < - 2   e   0 <   x < 2

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento acima

Exercícios de Livros Relacionados

Esboce o gráfico de cada uma das funções do exercício anterior.i) f x = ln ⁡ x x
Esboce o gráfico de cada uma das funções do exercício anterior.g) y = x 1 + x 2
Suponha que f^(' ') (x)0 em ]a , + oo[ e que existe x_0a tal que f^' (x_0)0 . Prove que underset(x - + oo)(lim) f (x) = + oo
Seja f derivável até a 2 ª ª ordem em R e tal que, para todo x , xf ' ' x + f ' x = 4 .a) Mostre que f ' ' é contínua em todo x ≠ 0 b) Mostre que f não admite ponto de inflexão horizontal
Sejam f uma função derivável até a 5 ª ª ordem no intervalo aberto I e p ∈ I . Suponha f ( 5 ) contínua em p . Prove que f ' ' p = f ' ' ' p = f 4 p = 0 e f 5 p ≠ 0 é uma condição suficiente para p se