Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Concavidade

Ver Teoria
Exercício 6312345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626465666768697071727374

Enunciado

UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 6.12b

Estude a concavidade e esboce os gráficos de:

b )   g x = x 1 + x 2

Passo 1

Olá pessoal, como vocês estão?

Nessa questão recebemos a função

g x = x 1 + x 2

E, precisamos estudar a concavidade dessa função, bem como esboçar o seu gráfico.

Para estudar a concavidade de uma função devemos analisar a sua segunda derivada. Se:

g ' ' x > 0 → c o n c a v i d a d e   p a r a   c i m a

g ' ' x < 0 → c o n c a v i d a d e   p a r a   b a i x o

g ' ' x = 0 → m u d a n n ç a   n a   c o n c a v i d a d e   ( p o n t o   d e   i n f l e x ã o )

Massa! Quanto ao esboço do gráfico, vamos focar principalmente na informação das concavidades para esboçá-lo, se preocupando mais com a forma geral da curva mesmo, beleza?

Vamo nessa!

Passo 2

Vamos começar calculando a derivada da nossa função.

Pela regra do produto, temos:

g ' x = x ' ⋅ 1 1 + x 2 + x ⋅ 1 1 + x 2 '

= 1 1 + x 2 - 2 x 2 1 + x 2 2

Logo:

g ' x = 1 - x 2 1 + x 2 2

Derivando mais uma vez, temos:

g ' ' x = - 2 x 1 + x 2 2 + 1 - x 2 - 2 ⋅ 2 x 1 + x 2 3

= - 2 x 1 + x 2 3 ⋅ ( 1 + x 2 + 2 - 2 x 2 )

⇒ g ' ' x = - 2 x 3 - x 2 1 + x 2 3

Muito bom!

Agora vamos fazer o estudo do sinal dessa função.

O denominador é sempre positivo.

1 + x 2 3 > 0

Logo, o sinal da função será determinado pelo numerador:

( - 2 x ) ( 3 - x 2 )

Temos o produto de dois termos, vamos analisar o sinal de cada um deles:

- 2 x > 0 ,     x < 0 < 0 ,     x > 0

( 3 - x 2 ) > 0 ,     - 3 < x < 3 < 0 ,     x < - 3   e   x > 3

Daí, fazendo as intersecções, temos:

x < - 3   ⇒ g ' ' x > 0 - 3 < x < 0 ⇒ g ' ' x > 0 0 < x < 3 ⇒ g ' ' x < 0 3 < x ⇒ g ' ' x > 0

Muito bom!

Resumindo melhor os intervalos em que a concavidade é para cima ou para baixo, temos:

- ∞ ,   0 ∪ 3 ,   + ∞ → c o n c a v i d a d e   p a r a   c i m a

0 , 3 → c o n c a v i d a d e   p a r a   b a i x o

Perfeito 😊

Passo 3

Agora vamos esboçar a nossa função.

Para isso devemos ficar ligados que, quando x → ± ∞ a função se aproxima do eixo x assintotando. Além disso, em x = 0 temos f x = 0 .

Começando pelo trecho ( - ∞ , 0 ) , temos:

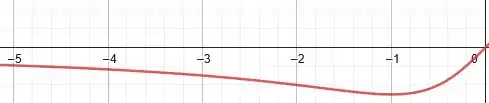
Já para x > 0 , temos uma mudança de concavidade tanto em x = 0 como em x = 3 . Daí:

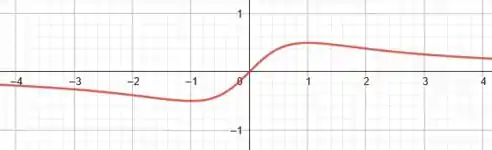
Prontinho gente!! Finalizamos mais uma questão 😊

Até a próxima!!

Resposta

Resposta no texto.

Exercícios de Livros Relacionados

Esboce o gráfico de cada uma das funções do exercício anterior.i) f x = ln ⁡ x x
Esboce o gráfico de cada uma das funções do exercício anterior.g) y = x 1 + x 2
Suponha que f^(' ') (x)0 em ]a , + oo[ e que existe x_0a tal que f^' (x_0)0 . Prove que underset(x - + oo)(lim) f (x) = + oo
Seja f derivável até a 2 ª ª ordem em R e tal que, para todo x , xf ' ' x + f ' x = 4 .a) Mostre que f ' ' é contínua em todo x ≠ 0 b) Mostre que f não admite ponto de inflexão horizontal
Sejam f uma função derivável até a 5 ª ª ordem no intervalo aberto I e p ∈ I . Suponha f ( 5 ) contínua em p . Prove que f ' ' p = f ' ' ' p = f 4 p = 0 e f 5 p ≠ 0 é uma condição suficiente para p se