UFES, Cálculo I, P2, 2020.2, questão 6c
Considere a função cuja derivada é
(c) os intervalos onde o gráfico de tem concavidade para cima ou para baixo
Passo 1
Faaaala, galeraaaa! Tudo belezinha?
Bom, para saber qual intervalo onde a concavidade da função é para cima ou para baixo, basta calcular a inequação da derivada segunda, quando .
Calculando a derivada segunda temos
Assim, podemos reescrever
Calculando a inequação, temos
Resolvendo a equação do segundo grau
Passo 2
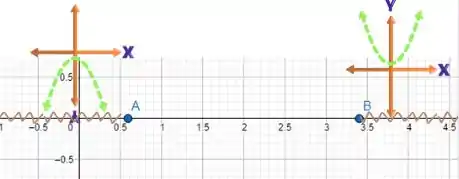
Por fim, podemos desenhar o intervalo em que a concavidade da função é para baixo ou para cima, como mostra a figura abaixo.
Logo, quando
Prontinho, até mais!
Resposta
Exercícios de Livros Relacionados
Esboce o gráfico de cada uma das funções do exercício anterior.i) f x = ln x x
Esboce o gráfico de cada uma das funções do exercício anterior.g) y = x 1 + x 2
Suponha que f^(' ') (x)0 em ]a , + oo[ e que existe x_0a tal que f^' (x_0)0 . Prove que underset(x - + oo)(lim) f (x) = + oo
Seja f derivável até a 2 ª ª ordem em R e tal que, para todo x , xf ' ' x + f ' x = 4 .a) Mostre que f ' ' é contínua em todo x ≠ 0 b) Mostre que f não admite ponto de inflexão horizontal
Sejam f uma função derivável até a 5 ª ª ordem no intervalo aberto I e p ∈ I . Suponha f ( 5 ) contínua em p . Prove que f ' ' p = f ' ' ' p = f 4 p = 0 e f 5 p ≠ 0 é uma condição suficiente para p se