- Considere a dada por e suas derivadas e
- Determine os intervalos nos quais o gráfico de é côncavo para cima e onde é côncavo para baixo.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós precisamos dizer quando o gráfico é côncavo para cima e para baixo. Para isso vamos analisar a nossa segunda derivada.
Para quem não lembra:
- Se , o gráfico é côncava para baixo.
- Se , o gráfico é côncava para cima.
Bora lá!
Passo 2
Então, galerinha, a o problema nos forneceu essa derivada,
Para facilitar a nossa análise, vamos dividi-la em duas partes: a primeira parte é e segunda parte é .
A parte exponencial é sempre positiva. Mas a outra parte é polinômio de segundo grau, então temos que descobrir quando ele é positivo ou negativo.
Como temos uma função do terceiro grau, vamos ter três raízes. De cara, temos que é uma solução para equação acima. Agora precisamos achar as outras duas raízes.
Vamos reescrever a nossa equação, colocando em evidencia
Opaa, agora podemos usar a parte para achar as outras duas raízes,
Agora temos os seguintes intervalos para analisar, , , e .
Agora vamos montar a nossa tabelinha!
Passo 3
Organizando os nossos dados e analisando o sinal da função em cada intervalo, ficamos com
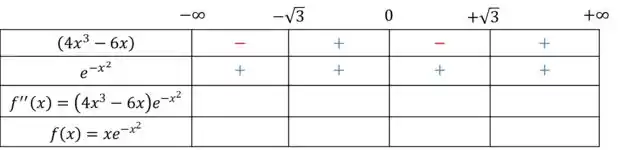
Fazendo o produto das duas partes da derivada, ficamos com
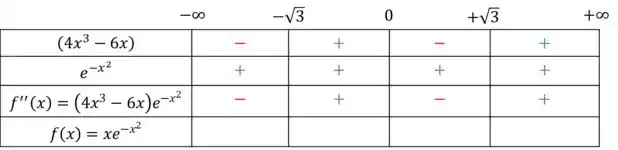
Agora, sabendo que quando a derivada é positiva, temos uma concavidade para cima; e quando ela é negativa, a concavidade para baixo, teremos:
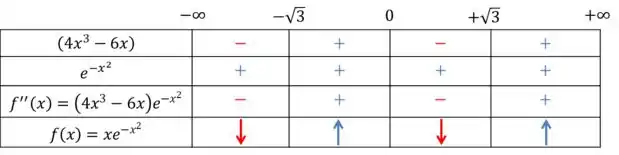
Resposta
- A concavidade é para cima em e .
- A concavidade é para baixo em e .