UFCG – Cálculo Diferencial e Integral I – Atividade Avaliativa 3 (AV3) – Parte 1 – 2022.2 – Questão 3c.
- Seja a função , determine:
- Os intervalos onde a função tem concavidade voltada para cima e concavidade voltada para baixo e os pontos de inflexão.
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão dá pra gente a função
e pede para gente dizer quais os intervalos onde a função tem concavidade voltada para cima e concavidade voltada para baixo e os pontos de inflexão.
Tá, mas como conseguiremos fazer isso???
O lance é o seguinte, podemos dizer que a função tem concavidade voltada para baixo quando a derivada segunda dela é menor que zero, e que a função tem concavidade voltada para cima quando a derivada segunda dela é maior que zero. E quem vai dividir os intervalos de sentido da concavidade é justamente o ponto de inflexão da função, que é onde ela muda de comportamento, e nesse ponto a derivada segunda da função é igual a zero.
Então, como você deve ter percebido, quem vai brilhar aqui hoje é justamente a nossa derivada segunda, então bora descobrir quem ela é!
Vem comigo que vamos fazer isso juntos.
Passo 2
A primeira coisa que devemos fazer é encontrar a derivada segunda da função e calcular o pondo de inflexão, que como dito antes, é o ponto onde a derivada segunda é igual a zero.
Assim, fazemos
E derivando a primeira vez, ficamos com:
Agora vamos derivar novamente, ficando com:
Para descobrir o ponto de inflexão, fazemos:
Assim,
Show, achamos um dos itens pedidos pela questão. Partiu agora saber qual o intervalo onde a concavidade da função está voltada para baixo e qual intervalo onde a concavidade da função está voltada para cima.
Passo 3
Acabamos de encontrar os pontos de inflexão, então vamos dividir nossos intervalos da seguinte forma:
Precisamos investigar qual o sinal da derivada segunda da função para valores menores que e para valores maiores que .
Para valores menores que .
Podemos substituir diretamente um valor menor que na derivada segunda da nossa função, como por exemplo o . Veja:
Então chegamos à conclusão que para valores menores que a derivada segunda da função é positiva, indicando que nesse intervalo a função tem concavidade voltada para cima.
tem concavidade voltada para cima.
Para valores maiores que . :
Podemos pegar o
Então chegamos à conclusão que para valores maiores que a derivada segunda da função é negativa, indicando que nesse intervalo a função tem concavidade voltada para baixo. E escrevemos que
tem concavidade voltada para baixo.
E pra confirmar tudo isso que calculamos, aí vai o gráfico da nossa função:
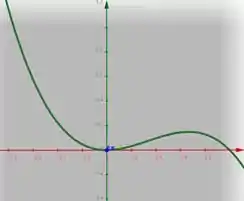
E prontinho. Problema resolvido. 😊
Partiu próxima?!
Resposta
ponto de inflexão.
tem concavidade voltada para cima.
tem concavidade voltada para baixo.