UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 6.14
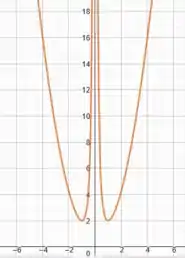
Esboce o gráfico de .
Passo 1
E aí galera, tudo tranquilo com voc��s?
Nessa questão recebemos a função:
E, precisamos esboçar o seu gráfico.
Para fazer isso vamos analisar a primeira derivada(para indicar o intervalo de crescimento, decrescimento e pontos críticos), o limite quando (para indicar a presença de assíntotas horizontais) e a continuidade da função.
A partir dessas informações já conseguimos esboçar o gráfico da nossa função 😊
Vamos nessa!
Passo 2
Temos:
Vamos começar calculando a primeira derivada:
Igualando a zero para encontrar os pontos críticos, temos:
Para saber se são pontos de máximo, mínimo ou inflexão, podemos calcular a segunda derivada nesses pontos.
Essa função é sempre positiva, logo:
Assim, esses são pontos de mínimo!
Além disso, como a segunda derivada é sempre positiva, dizemos que ela sempre tem concavidade para cima!
Passo 3
Vamos analisar agora a existência de assíntotas verticais ou horizontais.
Começando pelas horizontais, devemos calcular o limite de quando .
Pois o termo tenderá ao infinito. Assim, não há assíntota horizontal, a função cresce indefinidamente.
Analogamente:
Logo, a função também cresce indefinidamente para a esquerda.
Pensando agora na continuidade, como a função é dada por:
Temos a restrição do denominador, que precisa ser diferente de . Logo:
Vamos calcular o limite quando tende a e .
Pois, o termo .
Analogamente:
Assim, temos uma assíntota vertical em .
Passo 4
Juntando agora todas essas informações, já podemos esboçar o nosso gráfico.
A curva deve vir lá do altooo, tendendo a quando é muito negativo. E, vai diminuindo até encontrar o ponto de mínimo em . Depois ela volta a crescer e assintota a reta .
O lado à direita do eixo será simétrico.
Temos então:
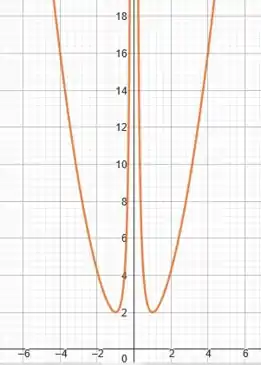
Prontinhoo! Terminamos 😊
Até a próxima pessoal!
Resposta
