Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Concavidade

Ver Teoria
Exercício 5412345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535556575859606162636465666768697071727374

Enunciado

UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 6.12a

Estude a concavidade e esboce os gráficos de:

a )   f x = e - x 2 / 2  

Passo 1

Fala aí pessoal, tudo bem?

Nessa questão recebemos a função

f x = e - x 2 2

E, precisamos estudar a concavidade dessa função, bem como esboçar o seu gráfico.

Para estudar a concavidade de uma função devemos analisar a sua segunda derivada. Se:

f ' ' x > 0 → c o n c a v i d a d e   p a r a   c i m a

f ' ' x < 0 → c o n c a v i d a d e   p a r a   b a i x o

f ' ' x = 0 → m u d a n n ç a   n a   c o n c a v i d a d e   ( p o n t o   d e   i n f l e x ã o )

Massa! Quanto ao esboço do gráfico, vamos focar principalmente na informação das concavidades para esboçá-lo, se preocupando mais com a forma geral da curva mesmo, beleza?

Vamo nessa!

Passo 2

Vamos começar calculando a derivada da função.

f ' x = e - x 2 2 '

= - x 2 2 ' ⋅ e - x 2 2

=   - x ⋅ e - x 2 2

Derivando mais uma vez:

f ' ' x = - x ⋅ e - x 2 2 '

=   - e - x 2 2 - x ⋅ - x ⋅ e - x 2 2

⇒ f ' ' x = x 2 - 1 ⋅ e - x 2 2

Muito bom!

Vamos agora estudar o sinal dessa função.

Algo importante pra gente ficar ligado aqui é que a função exponencial é sempre positiva.

Assim:

e - x 2 2 > 0

Logo, o sinal de f ' ' ( x ) vai ser determinado pelo sinal de ( x 2 - 1 ) .

x 2 - 1 < 0

x 2 < 1

Logo, f ' ' x < 0 (concavidade para baixo) se:

- 1 < x < 1

Caso:

x = ± 1

Temos f ' ' x = 0 , ou seja, pontos de inflexão.

E, se:

x < - 1   o u   x > 1

temos f ' ' x > 0 (concavidade para cima).

Massa!

Passo 3

Agora que já temos a informação sobre a concavidade da função, podemos esboçá-la.

Como já comentamos, a função exponencial é sempre positiva. Assim, ela estará sempre acima do eixo x .

Para - 1 < x < 1 , temos a concavidade para baixo. Além disso, em x = 0 , temos:

f x = e 0 = 1

Daí, podemos esboçar para esse trecho:

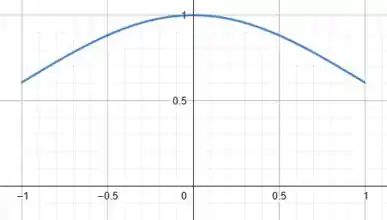
Para x < - 1 e x > 1 a concavidade da função é para cima.

E, quando x é muito grande, a função assume valores muito próximos de zero, pois:

f x = 1 e x 2 2

Ou seja, a exponencial está no denominador, e ela aumenta conforme x aumenta em módulo.

Daí, esboçando o restante da função, temos:

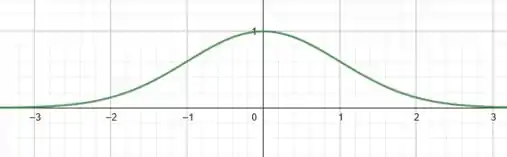
Prontinho! Curtiram a solução?

Responde Aí!

Resposta

Resposta no texto.

Exercícios de Livros Relacionados

Esboce o gráfico de cada uma das funções do exercício anterior.i) f x = ln ⁡ x x
Esboce o gráfico de cada uma das funções do exercício anterior.g) y = x 1 + x 2
Suponha que f^(' ') (x)0 em ]a , + oo[ e que existe x_0a tal que f^' (x_0)0 . Prove que underset(x - + oo)(lim) f (x) = + oo
Seja f derivável até a 2 ª ª ordem em R e tal que, para todo x , xf ' ' x + f ' x = 4 .a) Mostre que f ' ' é contínua em todo x ≠ 0 b) Mostre que f não admite ponto de inflexão horizontal
Sejam f uma função derivável até a 5 ª ª ordem no intervalo aberto I e p ∈ I . Suponha f ( 5 ) contínua em p . Prove que f ' ' p = f ' ' ' p = f 4 p = 0 e f 5 p ≠ 0 é uma condição suficiente para p se