UFPE – Cálculo 1 – 2020.2 – Segundo Exame – Exercício 4
Disserte sobre como as derivadas afetam a forma de um gráfico. O seu texto deve responder as seguintes perguntas:
I. O que diz sobre ?
II. O que diz sobre ?
Passo 1
Fala galerinha, beleza?
Esse problema é completamente teórico e vamos discutir um pouco o que as derivadas de uma função dizem sobre ela.
A primeira ideia que precisamos lembrar é que a derivada de uma função nada mais é que a taxa de variação da função . Uma analogia muito boa é pensar que descreve a posição de um corpo e sua derivada representa a velocidade, isto é, a taxa de variação da posição com relação ao tempo.
Se , a taxa de variação da função é positiva, de modo que um aumento da variável representará um aumento no valor da função. Isso significa que a função é crescente nessa região.
Da mesma forma, se , a taxa de variação é negativa, indicando que a função é decrescente nesse ponto, isto é, para um aumento no valor de , o valor da função diminui.
Além disso, se temos o chamado ponto crítico: é um ponto em que a reta tangente ao gráfico da função é horizontal e a taxa de variação da função é nula! Esses pontos podem ser pontos de máximo ou mínimo e tem grande importância no estudo das funções!
Passo 2
Assim como representa a taxa de variação de , podemos dizer que representa a taxa de variação de . Podemos dizer que é a taxa de variação da taxa de variação de . A analogia aqui é: enquanto representa a posição de um corpo e representa sua velocidade, é a aceleração.
Do ponto de vista gráfico, a segunda derivada dará informações sobre a concavidade do gráfico de .
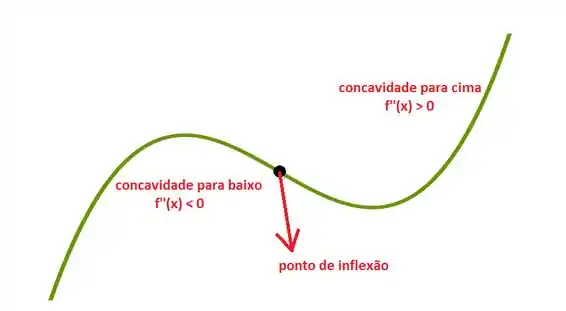
Se , a concavidade da função será para cima (pensa na parábola feliz). Já para , a concavidade será para baixo (parábola triste). Os pontos em que são chamados de pontos de inflexão: neles geralmente há uma mudança de concavidade!
Resposta
Explicação.