USP– Cálculo 1 – Lista 2 – Questão 1.6d
Seja uma função cuja derivada tem o gráfico esboçado na figura abaixo
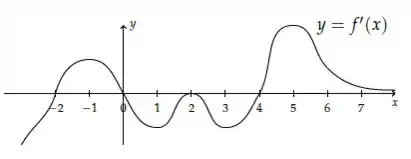
- Ache os pontos de inflexão de
Passo 1
Oi pessoal, tudo bem por aí? Essa questão nos dá o gráfico da função derivada de uma função
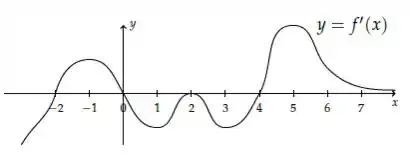
E faz um pedido
Ache os pontos de inflexão de
E agora, como determinar isso?
Sabemos que os pontos de inflexão são onde a derivada segunda troca de sinal, ou seja, quando a concavidade troca! Como temos o gráfico da derivada, precisamos identificar os pontos onde a derivada é zero (pontos de máximo e mínimo na função derivada). Esses serão nossos pontos de inflexão!
Beleza? Relaxa, vamos resolver juntos!
Bora lá!
Passo 2
Retomando o gráfico dado temos
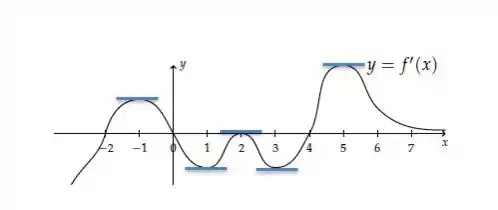
Temos cinco pontos em que a derivada (da função derivada, portanto a derivada segunda da função ) é zero
beleza? É isso!
Até a próxima!
Resposta
Exercícios de Livros Relacionados
Esboce o gráfico de cada uma das funções do exercício anterior.i) f x = ln x x
Esboce o gráfico de cada uma das funções do exercício anterior.g) y = x 1 + x 2
Suponha que f^(' ') (x)0 em ]a , + oo[ e que existe x_0a tal que f^' (x_0)0 . Prove que underset(x - + oo)(lim) f (x) = + oo
Seja f derivável até a 2 ª ª ordem em R e tal que, para todo x , xf ' ' x + f ' x = 4 .a) Mostre que f ' ' é contínua em todo x ≠ 0 b) Mostre que f não admite ponto de inflexão horizontal
Sejam f uma função derivável até a 5 ª ª ordem no intervalo aberto I e p ∈ I . Suponha f ( 5 ) contínua em p . Prove que f ' ' p = f ' ' ' p = f 4 p = 0 e f 5 p ≠ 0 é uma condição suficiente para p se