Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Concavidade

Ver Teoria
Exercício 1812345678910111213141516171920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374

Enunciado

Questão 2:

Considere a função

f x = ∫ 0 2 x + 2 t 2 e t   d t

  1. Determine a primeira e a segunda derivada de f .
  2. Determine as abscissas (coordenadas x ) dos pontos de inflexão do gráfico de f . Justifique sua resposta.
  3. Determine as ordenadas (coordenadas y ) dos pontos de inflexão de f .

Passo 1

a )

Então, vamos começar esse problema lembrando-se do teorema fundamental do cálculo que nos diz que...

f x = ∫ 0 v x f t   d t             →             f ' x = f v x ⋅ v ' x

Então, no nosso caso...

f x = ∫ 0 2 x + 2 t 2 e t   d t

A f t = t 2 e t e v x = 2 x + 2 ...

f ' x = f v x ⋅ v ' x

f ' x = 2 x + 2 2 e 2 x + 2 ⋅ 2 x + 2 '

f ' x = 2 2 x + 2 2 e 2 x + 2

Sacou?

Passo 2

Para a segunda derivada, basta derivar a primeira...

f ' ' x = f ' x '

f ' ' x = 2 2 x + 2 2 e 2 x + 2 '

Repare que vamos ter que aplicar em uma primeira instância, a regra do produto...

f ' ' x = 2 2 x + 2 2 ' e 2 x + 2 + 2 2 x + 2 2 e 2 x + 2 '

Derivando a primeira parcela aplicando a regra da cadeia...

f ' ' x = 2 ⋅ 2 2 x + 2 ⋅ 2 x + 2 ' e 2 x + 2 + 2 2 x + 2 2 e 2 x + 2 ' →

f ' ' x = 8 2 x + 2 e 2 x + 2 + 2 2 x + 2 2 e 2 x + 2 '

Calculando agora a derivada da segunda parcela (presta atenção, pois a use-as a regra da cadeia aqui também, onde a função mais externa é a exponencial, e a mais interna é a dos parênteses)...

f ' ' x = 8 2 x + 2 e 2 x + 2 + 2 2 x + 2 2 e 2 x + 2 2 x + 2 ' →

f ' ' x = 8 2 x + 2 e 2 x + 2 + 4 2 x + 2 2 e 2 x + 2

Colocando em evidência...

f ' ' x = e 2 x + 2 8 2 x + 2 + 4 2 x + 2 2     →

f ' ' x = e 2 x + 2 16 x + 16 + 4 4 x 2 + 8 x + 4 →

f ' ' x = e 2 x + 2 16 x + 16 + 16 x 2 + 32 x + 16   →

f ' ' x = e 2 x + 2 16 x 2 + 48 x + 32

Passo 3

b )

Bem, para encontrar possíveis pontos de inflexão o que fazemos é igualar a segunda derivada a zero e avaliar o zero da função...

f ' ' x = e 2 x + 2 16 x 2 + 48 x + 32       →           e 2 x + 2 16 x 2 + 48 x + 32 = 0

Bem, a exponencial nunca é zero, então se alguém zerar aí, esse alguém tem que ser...

16 x 2 + 48 x + 32 = 0

16 x 2 + 3 x + 2 = 0

x 2 + 3 x + 2 = 0

Calculando por Báskara...

x = - 3 ± 9 - 8 2           →                 x 1 = - 1 x 2 = - 2

Então, esses dois pontos são dois prováveis a pontos de inflexão. Vamos averiguar?

Passo 4

Para verificar isso, vamos estudar o sinal da segundo derivada...

f ' ' x = e 2 x + 2 16 x 2 + 48 x + 32

Bem, a exponencial é sempre positiva, então ela não contribui para o sinal da segunda derivada. Quem contribui é só a equação   16 x 2 + 48 x + 32 . Vamos chamar essa expressão de g x ...

g x = 16 x 2 + 48 x + 32

E estudar o sinal dela, que por acaso será o mesmo sinal de f ' ' x .

g x = 16 x 2 + 3 x + 2

Estudar o sinal de g x é bem tranquilo, afinal já encontramos os zeros dela ( x = - 1 e x = - 2 ). Como a parábola tem o a > 0 , então ela tem a concavidade pra cima...

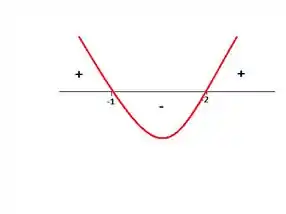
Então entre - 1 e - 2 a segunda derivada f ' ' x é negativa, o que significa que que a função f x tem a concavidade pra baixo entre - 1 e 2 .

De - ∞ a - 2 a g x é positiva e assim é f ' ' x , o que significa que nesse intervalo a f x tem uma concavidade pra cima, do mesmo jeito que de - 1 a + ∞ . Assim, só pode significar que a função f trocou de concavidade em - 1 e - 2 , logo esses caras são de fato pontos de inflexão ;)

Passo 5

c )

Bem, identificado o x , basta aplicar esses dois valores na expressão da função para determinar o y da coordenada dele...

x = - 1         →               y = f x = ∫ 0 2 x + 2 t 2 e t   d t         →

f - 1 = ∫ 0 0 t 2 e t   d t = 0

Então já descobrimos a ordenada do primeiro ponto... y = 0

Quanto ao segundo ponto...

Passo 6

x = - 2         →               y = f x = ∫ 0 2 x + 2 t 2 e t   d t       →

y = f - 2 = ∫ 0 2 - 2 + 2 t 2 e t   d t =

∫ 0 - 2 t 2 e t   d t

Então temos que calcular essa integral aí, e pra isso, usaremos a integração por partes... Tomamos o u como t 2 para ele reduzir a ordem...

u = t 2       →                   d u = 2 t d t

Enquanto isso, tomamos o d v ...

d v = e t d t           →                   v = e t

Aplicando na fórmula de integração por partes...

∫ u   d v = v u - ∫ v   d u

∫ t 2 e t   d t = t 2 e t - 2 ∫ t   e t

Precisamos de mais uma integração por partes para matar essa integral do lado direito agora...

u = t           →                 d u = d t

d v = e t         →                 v = e t

∫ t 2 e t   d t = t 2 e t - 2 t e t - ∫ e t d t

Essa integral que apareceu aí é moleza...

∫ t 2 e t   d t = t 2 e t - 2 t e t - e t

∫ t 2 e t   d t = t 2 e t - 2 t e t + 2 e t =

e t t 2 - 2 t + 2

Aplicando agora os limites de integração...

∫ 0 - 2 t 2 e t   d t = e t t 2 - 2 t + 2 0 - 2 =

e - 2 - 2 2 - 2 - 2 + 2 - e 0 0 2 - 2 0 + 2 =

10 e - 2 - 2 = 10 e 2 - 2

Essa é a ordenada do segundo ponto, x = - 2 .

Resposta

a )

f ' x = 2 2 x + 2 2 e 2 x + 2

f ' ' x = e 2 x + 2 16 x 2 + 48 x + 32

b ) x = - 1       e     x = - 2

c )   - 1 ,   0   e   - 2 ,   10 e 2 - 2

Exercícios de Livros Relacionados

Esboce o gráfico de cada uma das funções do exercício anterior.i) f x = ln ⁡ x x
Esboce o gráfico de cada uma das funções do exercício anterior.g) y = x 1 + x 2
Suponha que f^(' ') (x)0 em ]a , + oo[ e que existe x_0a tal que f^' (x_0)0 . Prove que underset(x - + oo)(lim) f (x) = + oo
Seja f derivável até a 2 ª ª ordem em R e tal que, para todo x , xf ' ' x + f ' x = 4 .a) Mostre que f ' ' é contínua em todo x ≠ 0 b) Mostre que f não admite ponto de inflexão horizontal
Sejam f uma função derivável até a 5 ª ª ordem no intervalo aberto I e p ∈ I . Suponha f ( 5 ) contínua em p . Prove que f ' ' p = f ' ' ' p = f 4 p = 0 e f 5 p ≠ 0 é uma condição suficiente para p se