UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.3.3d
Seja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
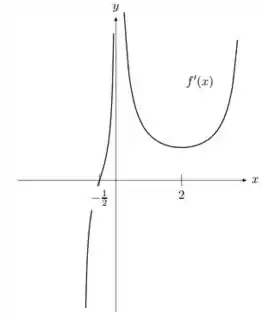
Responde o que se pede:
os intervalos onde o gráfico de possui concavidade para cima e onde possui concavidade para baixo.
Passo 1
Faaaala galera do nosso Brasil Varonil, como vocês estão?
Nessa questão temos uma função , com a informação de algum dos seus pontos:
Também foi dado o gráfico da derivada de , ou seja,
Nesse item precisamos determinar os intervalos do gráfico em que a concavidade da curva é para cima, e para baixo.
É importante a gente lembrar que a concavidade é determinada pela segunda derivada da função.
Assim, vamos analisar o gráfico de e verificar os intervalos em que é crescente (concavidade para cima), ou decrescente (concavidade para baixo).
Vamo nessa!
Passo 2
Vamos analisar o gráfico:
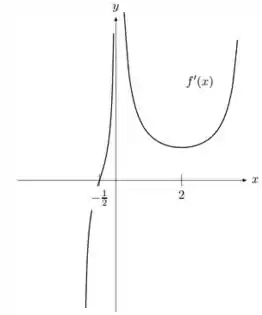
Em quais trechos a função é crescente?
Logo, nesse intervalo temos uma concavidade para cima em .
E, em quais trechos a função é decrescente?
Nesse intervalo temos uma concavidade para baixo.
Prontinho!
Valeu pessoal, até a próxima 😉