UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 8.1
Uma mosca está num arco de parábola . Descreva a parte desse arco no qual a mosca pode ficar a fim de não ser vista por um observador em .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos diz que uma mosca está no arco da seguinte parábola:
Sabendo disso, a questão nos pede para descrever a parte desse arco no qual a mosca pode ficar a fim de não ser vista por um observador em .
Para ficar mais fácil nossa visão, aqui está uma representação do que está acontecendo:
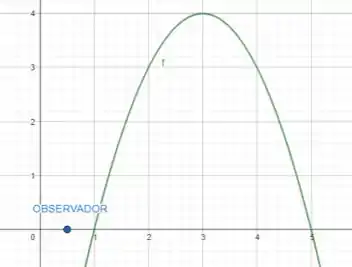
Bom... Para a mosca não ser vista pelo observador, ela precisa ficar em uma parte do arco de parábola que esteja "escondida" ou oculta pelo observador.
Nesse caso, a parte da parábola na qual a mosca pode ficar é a região que está abaixo da linha de visão do observador.
Mas como sabemos que linha é essa??
Bora junto descobrir??
😉
Passo 2
Bom... A linha de visão do observador é representada pela reta horizontal , pois ele está no ponto (coordenada ).
Nesse sentido, vamos encontrar os pontos de interseção entre a parábola e a linha de visão. Para isso, igualamos a zero na equação da parábola:
ou
Portanto, a mosca pode ficar na região entre os pontos e para não ser vista pelo observador, ou seja, na parte da parábola que está abaixo da linha de visão.
Entendeu direitinho? Responde aee ;)
Resposta
Entre os pontos e