Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Concavidade

Ver Teoria
Exercício 1912345678910111213141516171820212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374

Enunciado

Seja

f x = 2 x ln ⁡ x ,   x > 0

  1. f é crescente e seu gráfico é côncavo para cima quando x > 1 / 2 .
  2. f é decrescente e seu gráfico é côncavo para baixo quando x < 1 / 2 .
  3. f é crescente e seu gráfico é côncavo para baixo quando x > e - 1 .
  4. f é decrescente e seu gráfico é côncavo para baixo quando x > e - 1 .

Passo 1

Bem, a função é crescente, pois a medida que x aumenta e o ln ⁡ x também aumenta, sacou?

Agora, para buscarmos qual é o ponto onde a função muda de concavidade, busquemos os pontos de inflexão, calculando a segunda derivada e igualando a zero. Então vamos lá!

f x = 2 x ln ⁡ x         →             f ' x = ( 2 x ln ⁡ x ) '

Passo 2

Aplicando a regra do produto :

f ' x = 2 x ' ln ⁡ x + ln ⁡ x ' 2 x →

Derivando esses dois carinhas e sim, aplicando a regra da cadeia...

f ' x = 2 ln ⁡ x + 1 x 2 x   →

f ' x = 2 ln ⁡ x + 2  

Passo 3

Para estudarmos o sinal da função f , veja que primeiro é bom termos uma noção de quem é o gráfico dessa derivada

f ' x = 2 ln ⁡ x + 2  

O gráfico de 2 ln ⁡ x é basicamente o mesmo gráfico da l n (o dois multiplicando só estica o gráfico):

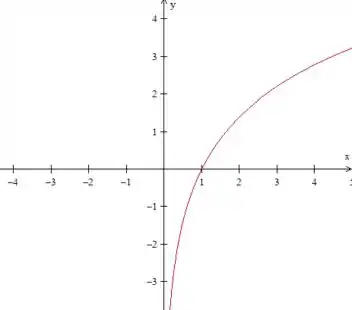
Se adicionarmos 2 em 2 ln ⁡ x , o que vamos fazer é deslocar o gráfico pra cima em duas unidades:

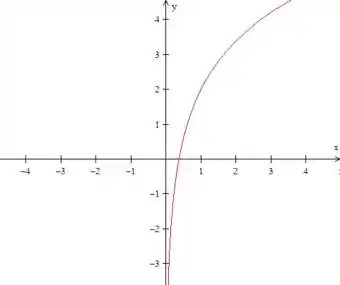
Esse é o gráfico da primeira derivada. Como ela passa por 0 em algum momento antes de 1 , vamos encontrar esse ponto crítico:

f ' x = 2 ln ⁡ x + 2               →               2 ln ⁡ x + 2 = 0

  2 ln ⁡ x = - 2           →

ln ⁡ x = - 1

Logo, pela definição de logaritmo:

x = e - 1 = 1 / e

Então acima de x = 1 / e , a função f é crescente, pelo fato do gráfico da primeira derivada ser positivo para valores acima desse cara!

Passo 4

Agora, calculemos a segunda derivada para sabermos onde é o ponto de inflexão!

f ' ' x = 2 ln ⁡ x + 2 ' →

f ' ' x = 2 x

Bem, note que para qualquer valor de x > 0 a segunda derivada é positiva, o que significa que a concavidade é sempre pra cima depois de 0 , em especial, depois de x > 1 / 2 .

Passo 5

Poxa! 1 / 2 é maior que 1 / e , pois Lembrando que e é aproximadamente 2 , 7 ...

2 , 7 > 2         →       I n v e r t e n d o   o s   n ú m e r o s   e   t a m b é m   o   s i n a l   …

1 2 , 7 < 1 2

Logo, quando estamos trabalhando com um x maior que meio, a função é crescente, por estarmos maior que 1 / e , e também ela tem a concavidade pra cima.

Excluindo todas as outas alternativas que fala o contrário, resta a letra a ...

Resposta

  1. f é crescente e seu gráfico é côncavo para cima quando x > 1 / 2 .

Exercícios de Livros Relacionados

Esboce o gráfico de cada uma das funções do exercício anterior.i) f x = ln ⁡ x x
Esboce o gráfico de cada uma das funções do exercício anterior.g) y = x 1 + x 2
Suponha que f^(' ') (x)0 em ]a , + oo[ e que existe x_0a tal que f^' (x_0)0 . Prove que underset(x - + oo)(lim) f (x) = + oo
Seja f derivável até a 2 ª ª ordem em R e tal que, para todo x , xf ' ' x + f ' x = 4 .a) Mostre que f ' ' é contínua em todo x ≠ 0 b) Mostre que f não admite ponto de inflexão horizontal
Sejam f uma função derivável até a 5 ª ª ordem no intervalo aberto I e p ∈ I . Suponha f ( 5 ) contínua em p . Prove que f ' ' p = f ' ' ' p = f 4 p = 0 e f 5 p ≠ 0 é uma condição suficiente para p se