UFCG – Cálculo Diferencial e Integral I – Atividade Avaliativa 3 (AV3) – Parte 1 – 2022.2 – Questão 1h.
- Defina:
- Concavidade do gráfico de uma função.
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão pede para definir o que é a concavidade do gráfico de uma função. Correto?
Mas o que é essa tal concavidade?
Vem comigo que te ajudo com isso.
Passo 2
Antes de falar quando uma função é côncava para cima ou para baixo, vamos relembrar o que é concavidade em si. A concavidade é a “concha” da função.
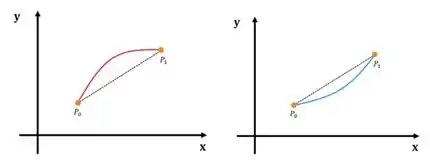
Chamamos a função à esquerda (em vermelho) de côncava para baixo e a da direita (em azul) de côncava para cima.
Nós temos nosso primeiro contato com esse assunto ainda quando estamos na escola, quando vemos os gráficos de funções de segundo grau. Você se lembra?
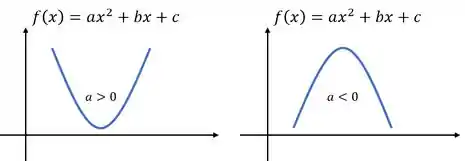
Nessa época nós podíamos definir a concavidade da função apenas olhando para o sinal do coeficiente da função.
Mas como faremos essa análise para funções que não são de segundo grau?
Vem que eu te mostro.
Passo 3
Em casos de funções mais difíceis, não temos como descobrir só batendo o olho nela, se a concavidade é para cima ou para baixo.
Para isso, podemos usar um truque que a derivada faz pra gente, é só seguir esses dois passos aqui:
1º Passo: Pega a função e deriva ela duas vezes, ou seja, pega a derivada segunda.
2º Passo: Estuda o sinal de , onde ela for positiva a concavidade vai ser para cima. E onde ela for negativa a concavidade é para baixo.
Então, assim podemos definir a concavidade de qualquer função que a tenha. 😊
E bora fazer mais uma questão?!!!
Resposta
No desenvolvimento.