UFCG – Cálculo Diferencial e Integral I – Atividade Avaliativa 3 (AV3) – Parte 1 – 2022.2 – Questão 1i.
- Defina:
- Ponto de inflexão.
Passo 1
Fala aí!!! Tudo belezinha com você? Bora desenvolver essa questão comigo?!
Bom, a questão pede para definir o que é o ponto de inflexão do gráfico de uma função. Correto?
Mas o que é essa tal inflexão?
Vem comigo que te ajudo com isso.
Passo 2
O ponto de inflexão de uma função pode ser entendido como o ponto onde a função troca de concavidade, ou seja, ela muda seu comportamento, se a concavidade estava pra cima, passa a ser pra baixo, e vice-versa. Mas e como eu acho esse ponto?
Muito simples. Basta achar as raízes da derivada segunda! Ela nos informa bastante coisa, como por exemplo a classificação dos pontos críticos de uma função dizendo se ele é um ponto de mínimo e a concavidade é para cima com , e se ele é um ponto de máximo e a concavidade é para baixo com . Mas quando diremos que esse é um ponto de inflexão.
Um exemplo bacana de concavidade é a função . Dá pra enxergar direitinho que a concavidade dela muda na origem:
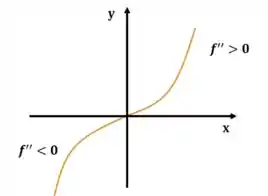
Pois temos que e, portanto, . Agora, qual o valor de pra que ? Ou seja, qual a raiz de ?
Nesse caso, a raiz da derivada segunda, , é . Assim, o ponto é um ponto de inflexão pra função . Então, como podemos ver no desenho, esse é o ponto onde a concavidade muda: antes era para baixo, depois foi para cima.
Pegou a ideia direitinho? Então fechou!!! Partiu próxima questão!
Resposta
No desenvolvimento.