UnB - Cálculo 1 - Listas- Lista 8 - Questão 10
O que significa dizer que é um ponto crítico de ?
Passo 1
E aiii, xuxus!! Quais as novidades? A que eu tenho pra vocês é que vão tirar 10 nessa matéria :)
Bora lá, a questão deseja saber o que significa afirmar que determinado é um ponto crítico de uma função . E aí? o que vocês me dizem, hein?
Passo 2
Bom galeraaa, já que vocês pensaram um pouquinho vamos definir de maneira bem simples o que vem a ser um ponto crítico. Um ponto crítico de uma função derivável é um ponto
do domínio de no qual ou então quando não existir. Em outras palavras um ponto crítico de uma função
é um ponto onde a derivada da função nesse ponto é igual a zero ou então é um ponto onde a derivada não existe.
Imaginemos que a nossa função se trata da função :
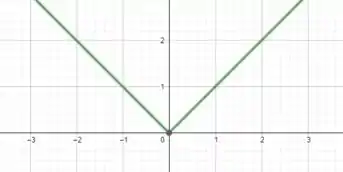
O gráfico dessa nossa função hipotética teria que ponto crítico?
Se você respondeu “Quando for igual a ”, você arrasou! É exatamente nesse ponto do gráfico que temos um ponto crítico devido ao fato da derivada não existir.
E aí, consegui te ajudar?? Responde Aí!
Bons Estudos pimpolhos! Xero :)
Resposta
Resolução nos passos acima