UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 9, Questão 9b
Determine para que valores de as expressões abaixo fazem sentido (em ):
b)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu a raiz de um quociente de equações e pediu pra gente encontrar os valores de para os quais ela está definida no conjunto dos números reais (em ).
Uma raiz de índice par, precisa ser teu seu radicando maior ou igual a zero, certo? Então, pra que esteja definida em , temos a condição:
Assim, o que nós vamos fazer é verificar as condições para que essa inequação seja verdade, avaliando os sinais de cada equação separadamente, em cada condição de desigualdade. Em seguida, nós vamos montar uma tabelinha e fazer o estudo de sinais.
Vamos lá!
Passo 2
Vamos começar fatorando as equações em cima e embaixo pra ficar mais tranquilo de resolver:
Para que seja maior ou igual a zero, precisamos que numerador e denominador tenham sinais iguais (lembrando que o denominador nunca pode ser zero). Então, num primeiro caso, temos:
Da primeira desigualdade, temos três retas:
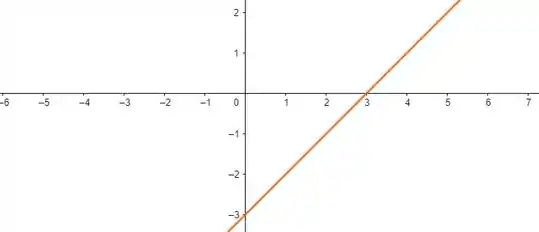
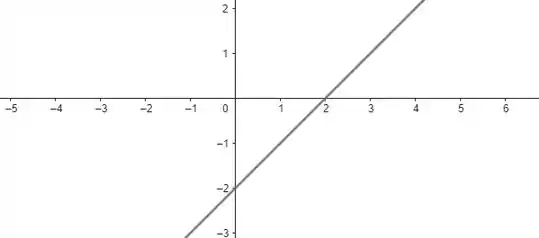
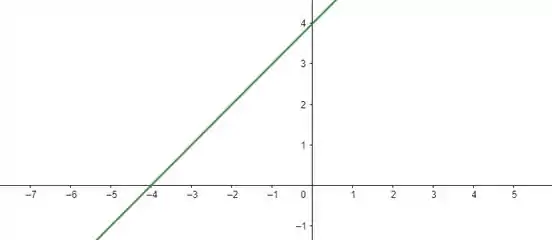
Nós estamos interessados nos locais onde essas funções são positivas. Repara que elas só são positivas depois de atravessar o eixo . Juntando tudo em um conjunto, temos os intervalos:
Da segunda desigualdade:
Temos as retas:
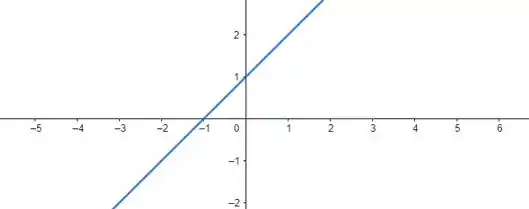
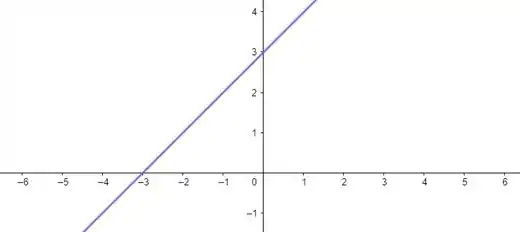
Que são positivas em:
Passo 3
Mas também pode ser maior ou igual a zero se:
A raízes e os gráficos são os mesmos nesse caso. O que muda são os intervalos que nós estamos interessados. Por exemplo, pra primeira desigualdade, queremos saber onde a função é negativa ou nula, olhando no gráfico do passo anterior, nós vemos que isso acontece em:
E pra segunda equação queremos os valores onde a função é apenas negativa. Isso acontece em:
Agora vamos estudar os sinais nesses intervalos e ver o que temos:
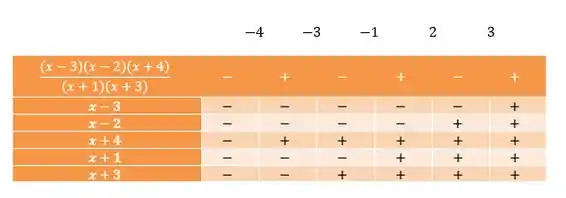
Lembra que nós definimos no passo :
Então, vamos selecionar os intervalos em que é positivo ou nulo. Olhando pra primeira linha da tabela, isso acontece em:
Que é nosso conjunto solução.
Prontinho, galera! Até a próxima! 😉