UFU – Cálculo 1 – Lista 1 – Questão 1c
Resolva as desigualdades
Passo 1
Oi pessoal, tudo bem? Vamos começar?
O problema começa nos dando essa desigualdade aqui
E agora, como resolver?
Bom, podemos trazer tudo para o lado esquerdo e ficamos com
Precisamos verificar onde esse produto retorna números positivos! Precisamos analisar o sinal de e de , para depois comparar os resultados
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossa desigualdade é
Analisando individualmente e temos
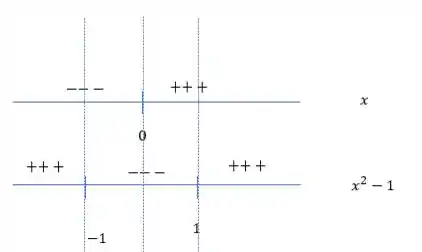
Beleza?
Agora nossa missão é fazer o produto do sinal dos termos para descobrir qual é o sinal referente ao intervalo! Lembrando que queremos onde o produto é positivo
Passo 3
Nossa desigualdade
Analisando o sinal em torno das raízes e comparando temos:
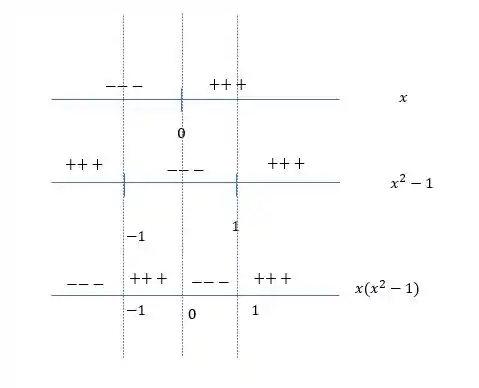
Tranquilo?
Nossos intervalos de interesse são onde a função retorna números positivos
Beleza? Espero ter ajudado!
Até a próxima!