Resolva em as inequações abaixo:
e) .
f) .
Passo 1
Eaí pessoal, tudo na paz?
Nessa questão temos duas inequações bem divertidas pra resolver haha. Começando pelo item a), temos:
Nesses casos com vários monômios se multiplicando, precisamos analisar o sinal um por um, e depois fazer o estudo do sinal.
Começando por:
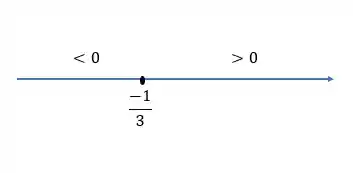
Como o expoente é ímpar, podemos ter valores negativos.
Se:
teremos
caso contrário, temos .
Portanto:
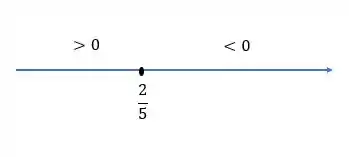
Fazendo a mesma análise para o próximo termo, com o expoente é negativo, temos:
Se:
Então, . Caso contrário, será menor ou igual a zero. Assim:
Analisando o último termo, vemos que como tem expoente par, não importa o valor que assumir essa expressão sempre será positiva.
Vamos então fazer o estudo do sinal:
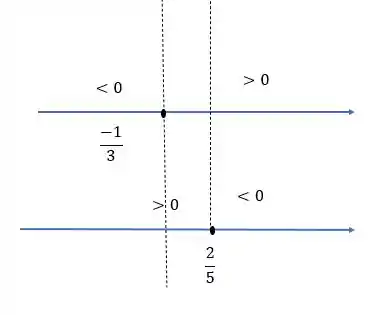
Logo, para que nossa inequação seja negativa, devemos ter:
Prontinho!
Passo 2
Nesse próximo item o raciocínio é bem semelhante. Agora temos:
A diferença é que temos dois termos com expoente positivo: e .
Assim, para eles não importa o valor que assumir, a expressão sempre será positiva.
Sendo assim, o sinal do produto desses termos ficará em cargo do termo:
Já que o seu expoente é ímpar, vale que se:
Como para a inequação queremos que seja menor ou igual a zero, ou seja, o primeiro caso. Temos:
Portanto, essa é a solução! Teremos:
Se .
Prontinho gente! Matamos mais uma questão!
Obrigado pela atenção e até a próxima 😊
Resposta
a)
b)