Resolva em as inequações abaixo:
a)
b)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu algumas inequações (que são equações que não possuem igualdade, lembra?) e pediu pra gente resolver dentro do conjunto dos número reais, ou seja, em . Tá, mas como a gente resolve isso?
Como temos inequações do segundo grau (onde o expoente de é ), resolve-las significa encontrar os valores de que satisfazem essa condição de desigualdade. No nosso caso, a condição no item a) é:
E no item b):
Nós aprendemos que as equações do segundo grau formam uma parábola e nas inequações não é diferente. Nós estamos interessados em saber onde elas serão positivas ou negativas. Mas como vamos resolver isso?
Primeiro vamos encontrar os valores onde nossa equação é igual a zero, que serão os pontos onde o nosso gráfico encosta no eixo . Depois nós vamos determinar o crescimento da função observando o coeficiente do e, em seguida, estudar os sinais do gráfico para definir o nosso conjunto solução.
Vamos lá!
Passo 2
Começando com o item a, onde temos:
Para a nossa equação, temos:
Encontrando as raízes dessa equação usando Bhaskara:
Opaaa! Teríamos uma raíz negativa.

Calma, vamos pensar na equação. Olhando pro valor de (que é o coeficiente de ), temos , um valor positivo. Isso significa que a nossa função sempre será positiva. O esboço do nosso gráfico fica assim:
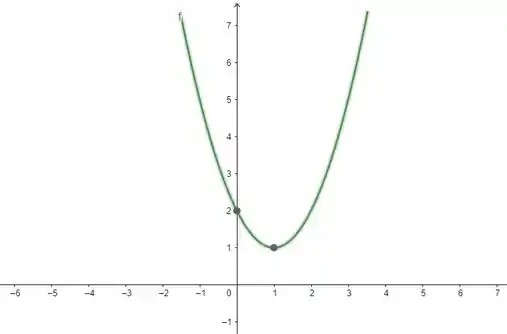
Como enunciado quer saber os valores de que tornam essa equação positiva, a resposta é todos haha. Porque a função é sempre positiva. Assim, o nosso conjunto solução será:
Passo 3
Agora vamos analisar a letra b):
O primeiro passo é tentar encontrar as raízes da equação do segundo grau:
Usando Bhaskara:
Temos as raízes:
Olhando agora pra nossa função, nós temos . Como o coeficiente é negativo, a nossa parábola fica virada para baixo:
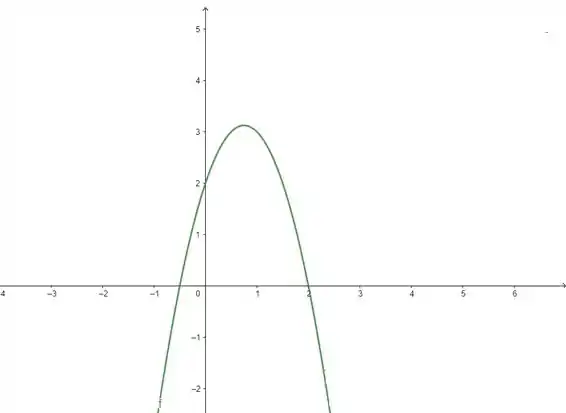
Repare que ela é negativa até , quando cruza o eixo . Depois passa a ser positiva até , quando cruza novamente o eixo .
Como enunciado quer saber os valores de que tornam essa equação maior ou igual a zero, a gente inclui as raízes encontradas e temos o conjunto solução onde a função é positiva:
Prontinho, galera! Até a próxima! 😉
Resposta
a)
b)