UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 8, Questão 8cde
Resolva em as inequações abaixo:
c)
d)
e)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu algumas inequações e pediu pra gente encontrar os valores de que elas podem assumir dentro do conjunto dos números reais.
Assim, o que nós vamos fazer é verificar as condições para que essa inequação seja verdade, avaliando os sinais de cada equação separadamente. Em seguida, nós vamos montar uma tabelinha e fazer o estudo de sinais.
Vamos lá!
Passo 2
Vamos começar avaliando a letra c):
Vamos olhar a primeira função , sua raiz será:
Como o é positivo na equação, a função é crescente e será negativa antes da raiz e positiva depois. Temos o seguinte gráfico:
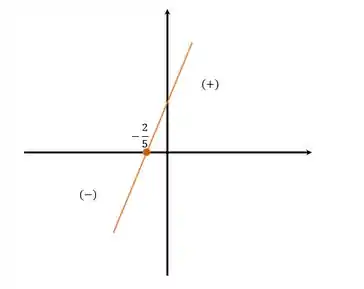
Já pra segunda parte, teremos como raiz:
Como é negativo, a função é decrescente e será positiva antes da raiz, e negativa depois, como mostra o gráfico:
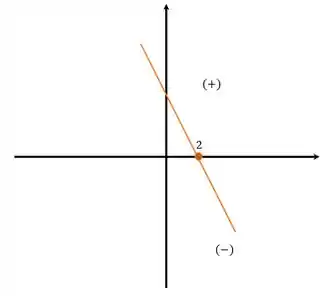
E por fim, temos:
Novamente a função é crescente, negativa antes da raiz e positiva depois.
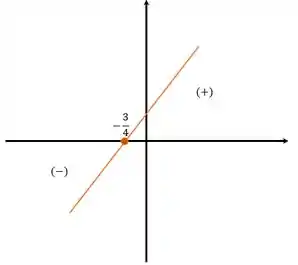
Agora vamos juntar as três partes pra fazer o quadro de sinais:
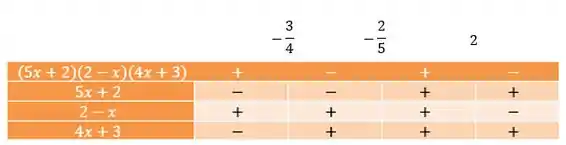
Como a condição da nossa inequação é que ela seja maior do que zero (positiva), vamos olhar na primeira linha da tabela os intervalos onde a função é positiva. Encontramos assim nosso conjunto solução:
Passo 3
Vamos avaliar a letra d) agora:
Olhando a primeira função , temos a raiz:
Como é negativo, a função é decrescente e será positiva antes da raiz, e negativa depois, como mostra o gráfico:
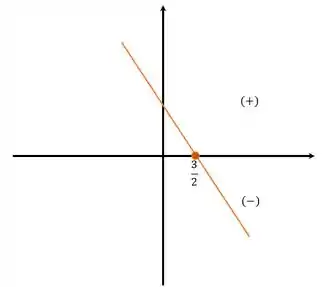
Já pra segunda parte, teremos como raiz:
Como é positivo, a função é crescente e será negativa antes da raiz, e positiva depois, como mostra o gráfico:
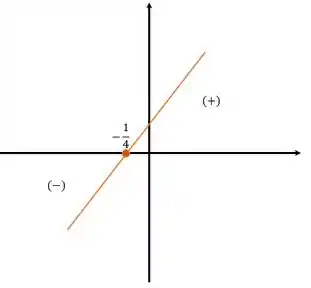
E por fim, temos:
Novamente a função é crescente, negativa antes da raiz e positiva depois.
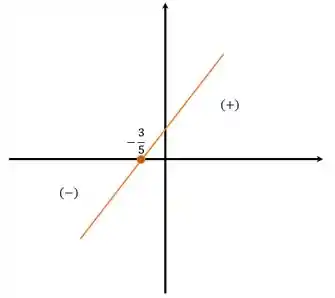
Agora vamos juntar as três partes pra fazer o quadro de sinais:
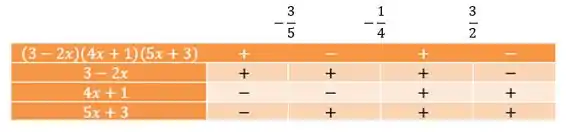
Como a condição da nossa inequação é que ela seja maior ou igual a zero, vamos olhar na primeira linha da tabela os intervalos onde a função é positiva e incluir as raízes no intervalo. Assim, temos nosso conjunto solução:
Passo 4
No item e), temos:
Pra o primeiro termo é negativo, a gente pode multiplicar a função por e inverter o sinal da desigualdade:
Agora vamos analisar cada termo. Pra o primeiro termo, temos a raiz:
Então, a função passa pela origem e até zero é negativo, depois passa a ser positivo.
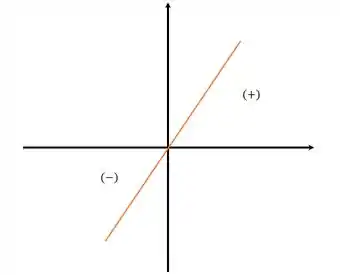
Para , temos:
A função é crescente, negativa antes da raiz e positiva depois, como mostra o gráfico:
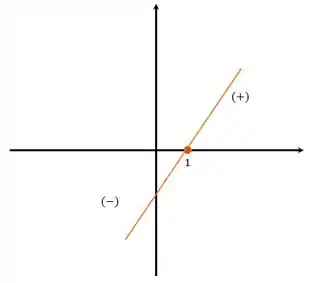
Para , temos:
A função é decrescente, porque o é negativo. Assim, ela é positiva antes da raiz e negativa depois:
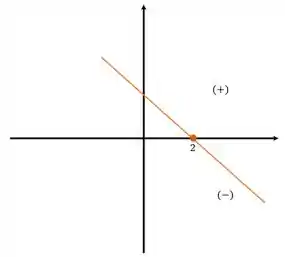
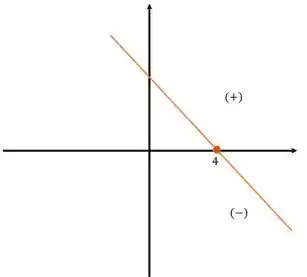
Para , temos:
A função é crescente, negativa antes da raiz e positiva depois:
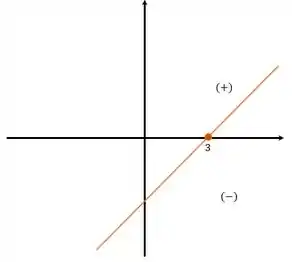
Por fim, temos:
A função agora é decrescente, positiva antes da raiz e negativa depois:
Juntando tudo no nosso quadro de sinais, temos:
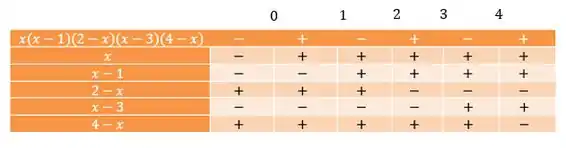
Olhando pra primeira linha da tabela, temos os intervalos onde a nossa inequação é negativa, já que a gente tá interessado na condição da função ser menor do que zero. Assim, temos o conjunto solução:
Prontinho, galera! Até a próxima! 😉
Resposta
c)
d)
e)