Resolva em as inequações abaixo:
c)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma inequação de quarto grau e pediu pra gente encontrar os valores de para os quais ela está definida no conjunto dos números reais (em ).
Então, nós precisamos encontrar os valores onde a função é negativa. Pra facilitar nossa vida e nos ajudar a verificar os sinais da função, vamos primeiro fazer a fatoração da equação e escrever ela como um produto. Em seguida, vamos verificar as raízes da equação e fazer o estudo de sinais.
Vamos lá!
Passo 2
Vamos começar fatorando a expressão:
Chegamos no produto:
Agora vamos analisar cada equação.
Para , temos:
Para , temos:
Para e os gráficos são bem parecidos, mas só nos interessa saber onde eles são positivos ou negativos. Pra isso, temos:
Então, nós sabemos que a função muda de sinal quando atravessa o eixo . Como acontece antes de Vamos analisar cada intervalo pra ficar mais claro.
Passo 3
Verificando cada termo, vamos juntar todos os intervalos numa tabelinha e estudar o sinal das equações:
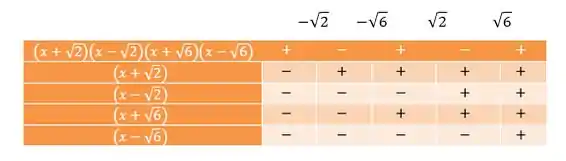
Como queremos:
Vamos selecionar os valores de nos intervalos que satisfaçam a desigualdade (olhando pra primeira linha da tabela). Dessa forma, temos:
Prontinho. Valeu, galera! 😉