UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 9, Questão 4ij
Resolva em as inequações abaixo:
i)
j)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu algumas inequações envolvendo módulo e pediu pra gente encontrar os valores de para os quais ela está definida no conjunto dos números reais (em ).
Existe um teorema que nós vamos usar muito, que nos diz que se pertence a e é um número real positivo, então nós podemos escrever na forma:
Sendo assim, o que nós vamos fazer é sempre tentar escrever a inequação nessa forma para encontrar o intervalo onde tá variando, beleza?
Vamos lá!
Passo 2
No item i), temos a inequação:
Repara que nós temos uma equação do segundo grau dentro do módulo, então nós vamos precisar encontrar suas raízes e esboçar seu gráfico pra estudar os sinais. Mas antes, vamos escrever o módulo conforme o teorema:
Vamos avaliar cada caso, começando com . Subtraindo dos dois lados:
Vamos calcular as raízes dessa equação:
Que nos dá:
Esboçando seu gráfico agora, temos:
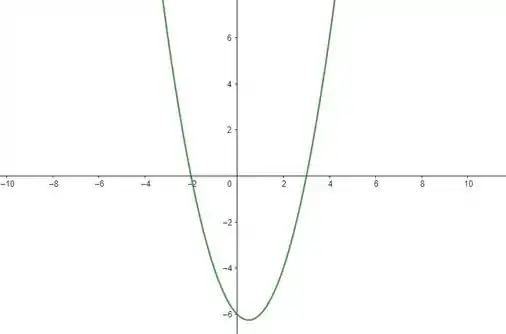
Lembra que a inequação que nós estamos avaliando é maior do que zero? Então, vamos olhar para os valores onde a função é positiva. Repare que é começa positiva, até , passa a ser negativa e depois volta a ser positiva em . Então, os valores que satisfazem nossa inequação estão no conjunto:
E quando ? Nesse caso, temos:
Calculando as raízes da equação:
Encontramos:
Esboçando seu gráfico:
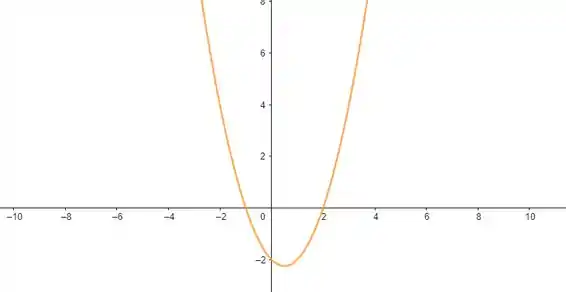
Nossa inequação agora é menor do que zero, então estamos interessados nos valores em que a função é negativa. Isso acontece quando ela tá abaixo do eixo , de até . Logo, temos o conjunto:
Juntando tudo, encontramos nossa solução geral para a inequação modular:
Vamos para a próxima!
Passo 3
Na letra j), nós temos:
Usando a propriedade do passo , temos:
Vamos avaliar a primeira desigualdade e começar somando dos dois lados:
Colocando tudo no mesmo denominador:
Agora precisamos pensar: o que faria esse quociente ser negativo (menor do que zero)? Se o numerador e o denominador tivessem sinais diferente, certo? Então, vamos fazer primeiro:
Daí, nós teríamos maior que e menor que . Mas isso não seria possível, porque . Então, vamos ver a outra possibilidade:
Agora sim, tudo ok. E a gente tem:
Passo 4
Agora vamos analisar a outra desigualdade:
Subtraindo dos dois lados:
Colocando tudo no mesmo denominador:
Multiplicado por dos dois lados, nós invertemos os sinais:
Agora vamos analisar de novo, o que faz o quociente ser negativo. Nós já sabemos que os sinais do numerador e do denominador precisam ser diferentes. Vamos testar a primeira possibilidade:
Até aqui, tudo ok. Teríamos o intervalo . Agora vamos testar a outra possibilidade:
Não tem como ser menor que e maior que ao mesmo tempo. Então, nosso conjunto é vazio nesse caso, e ficamos apenas com:
Juntando e temos o conjunto solução da inequação :
Valeu, galera! 😉
Resposta
i)
j)